题目内容
11.计算(1)2$\sqrt{12}$-6$\sqrt{\frac{1}{3}}$+3$\sqrt{48}$
(2)($\sqrt{48}$+$\frac{1}{4}$$\sqrt{6}$)÷$\sqrt{27}$.
分析 (1)根据二次根式的混合运算顺序,首先计算开方,然后计算乘法,最后从左向右依次计算即可.
(2)首先计算开方,然后分别用小括号里面的数除以3$\sqrt{3}$,再把所得的结果求和,即可求出算式($\sqrt{48}$+$\frac{1}{4}$$\sqrt{6}$)÷$\sqrt{27}$的值是多少.
解答 解:(1)2$\sqrt{12}$-6$\sqrt{\frac{1}{3}}$+3$\sqrt{48}$
=2×2$\sqrt{3}$-6×$\frac{\sqrt{3}}{3}$$+3×4\sqrt{3}$
=4$\sqrt{3}$-2$\sqrt{3}+12\sqrt{3}$
=14$\sqrt{3}$;
(2)($\sqrt{48}$+$\frac{1}{4}$$\sqrt{6}$)÷$\sqrt{27}$
=(4$\sqrt{3}$+$\frac{1}{4}$$\sqrt{6}$)÷3$\sqrt{3}$
=4$\sqrt{3}$$÷3\sqrt{3}$+$\frac{1}{4}$$\sqrt{6}$÷3$\sqrt{3}$
=$\frac{4}{3}$$+\frac{\sqrt{2}}{12}$.
点评 此题主要考查了二次根式的混合运算,要熟练掌握,解答此题的关键是要明确:①与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的.②在运算中每个根式可以看做是一个“单项式”,多个不同类的二次根式的和可以看作“多项式”.

练习册系列答案
相关题目
5.将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( )
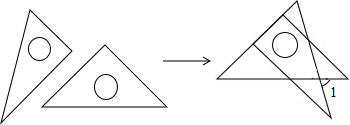

| A. | 75° | B. | 60° | C. | 45° | D. | 30° |
6.下列计算正确的是( )
| A. | (a2)3•a4=a9 | B. | -b•(-b)3=-b4 | C. | (a-b)•(-a-b)=-a2+b2 | D. | (3x-1)(x+3)=3x2-3 |
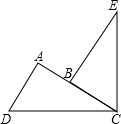 如图,已知:∠DAC=90°,∠EBC=90°,AD=BC,EC=DC,求证:AC=BE.
如图,已知:∠DAC=90°,∠EBC=90°,AD=BC,EC=DC,求证:AC=BE.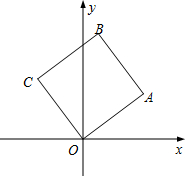 如图,正方形OABC的顶点O在坐标原点,且OA边和AB边所在直线的解析式分别为y=$\frac{3}{4}$x和y=-$\frac{4}{3}$x+$\frac{25}{3}$.
如图,正方形OABC的顶点O在坐标原点,且OA边和AB边所在直线的解析式分别为y=$\frac{3}{4}$x和y=-$\frac{4}{3}$x+$\frac{25}{3}$.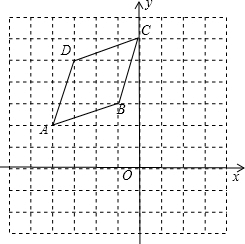 如图,平面直角坐标系中,菱形ABCD的四个顶点都在正方形网格的格点上.
如图,平面直角坐标系中,菱形ABCD的四个顶点都在正方形网格的格点上. 如图,B,C是线段AD上任意两点,M是AB的中点,N是CD中点.
如图,B,C是线段AD上任意两点,M是AB的中点,N是CD中点.