题目内容
11．
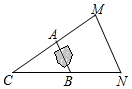如图，A，B两点被池塘隔开，不能直接测量其距离．于是，小明在岸边选一点C，连接CA，CB，分别延长到点M，N，使AM=AC，BN=BC，测得MN=200m，则A，B间的距离为100m．
分析 根据三角形中位线定理计算即可．
解答 解：∵AM=AC，BN=BC，
∴AB是△ABC的中位线，
∴AB=$\frac{1}{2}$MN=100m，
故答案为：100．
点评 本题考查的是三角形的中位线定理的应用，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
1．
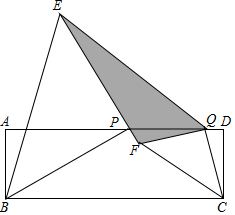如图，矩形ABCD中，BC=6，P，Q是边AD上的动点，PQ=2，△BPE和△CQE均为等腰直角三角形（点B，P，E和C，Q，E均按逆时针顺序排列），∠BPE=∠CQF=Rt∠，则图中阴影部分的面积为（ ）
如图，矩形ABCD中，BC=6，P，Q是边AD上的动点，PQ=2，△BPE和△CQE均为等腰直角三角形（点B，P，E和C，Q，E均按逆时针顺序排列），∠BPE=∠CQF=Rt∠，则图中阴影部分的面积为（ ）| A． | 2 | B． | 4 | C． | 6 | D． | 8 |
2．
如图所示的立方体，如果把它展开，可以是下列图形中的（ ）
如图所示的立方体，如果把它展开，可以是下列图形中的（ ）| A． |  | B． |  | C． |  | D． |  |
19．
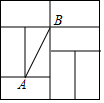如图是由8个全等的矩形组成的大正方形，线段AB的端点都在小矩形的顶点上，如果点P是某个小矩形的顶点，连接PA、PB，那么使△ABP为等腰直角三角形的点P的个数是（ ）
如图是由8个全等的矩形组成的大正方形，线段AB的端点都在小矩形的顶点上，如果点P是某个小矩形的顶点，连接PA、PB，那么使△ABP为等腰直角三角形的点P的个数是（ ）| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
6．用量角器测得∠MON的度数，下列操作正确的是（ ）
| A． |  | B． |  | ||
| C． |  | D． |  |
如图，A、B、C是⊙O上的三点，且四边形OABC是菱形．若点D是圆上异于A、B、C的另一点，则∠ADC的度数是60°或120°．
3．如图，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿虚线剪开，拼成右边的矩形．根据图形的变化过程写出的一个正确的等式是（ ）
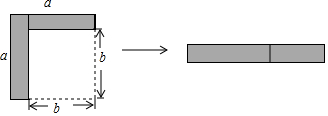
| A． | （a-b）2=a2-2ab+b2 | B． | a（a-b）=a2-ab | C． | （a-b）2=a2-b2 | D． | a2-b2=（a+b）（a-b） |
如图，已知四边形ABCD内接于半径为4的⊙O中，且∠C=2∠A，则BD=4$\sqrt{3}$．