题目内容
3．
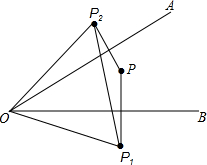如图，已知∠AOB=30°，点P在∠AOB的内部，点P1与点P关于OB对称，点P2与点P关于OA对称．求证：点P1，O，P2三点所构成的三角形是等边三角形．
分析 根据轴对称的性质，结合等边三角形的判定求解．
解答 证明：∵P为∠AOB内部一点，点P关于OB、OA的对称点分别为P1、P2，
∴OP=OP1=OP2且∠P1OP2=2∠AOB=60°，
∴△OP1P2是等边三角形，
即点P1，O，P2三点所构成的三角形是等边三角形．
点评 此题考查了轴对称的性质，对应点的连线与对称轴的位置关系是互相垂直，对应点所连的线段被对称轴垂直平分，对称轴上的任何一点到两个对应点之间的距离相等，对应的角、线段都相等．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
15．根据等式的性质，下列各式变形正确的是（ ）
| A． | 由$\frac{x}{5}$=20得x=4 | B． | 由3x-2=2x+2得x=4 | ||
| C． | 由2x-3=3x得x=3 | D． | 由3x-5=7得3x=7-5 |
如图，在△ABC中，点B关于AD的对称点B，在边AC上，DE⊥AB，DF⊥AC，请用刻度尺测量DE，DF，你能猜测两者之间有什么数量关系吗？请说明理由．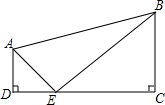
如图，在四边形ABCD中，AD∥BC，∠C=∠D=90°，AD=2，BC=3，CD=7，若点E是边DC上的一个动点，当DE为何值时，△EAD与△EBC相似？
如图所示，已知△ABC，过点A作直线l，求作△A′B′C′，使它与△ABC关于l对称，写出作图步骤并作图．
如图，在△ABC中，AB=AC，D为AC上一点，E为AB上一点，且BD=BC，AD=DE=BE，试求△ABC各内角的度数．
13．若|a|=2，|b|=3，且a＞b，则a+b=（ ）
| A． | -1 | B． | -5 | C． | -1或-5 | D． | 以上答案都不对 |