题目内容
15.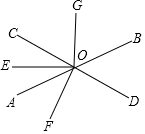 如图,直线AB与CD相交于O,OE是∠AOC的平分线,OF⊥CD,OG⊥OE,∠BOD=52°.
如图,直线AB与CD相交于O,OE是∠AOC的平分线,OF⊥CD,OG⊥OE,∠BOD=52°.(1)求∠AOF的度数;
(2)求∠EOF与∠BOG是否相等?请说明理由.
分析 (1)直接利用垂直的定义结合对顶角的定义得出∠AOF的度数;
(2)分别求出∠EOF与∠BOG的度数进而得出答案.
解答 解:(1)∵OF⊥CD,
∴∠COF=90°,
又∵∠AOC与∠BOD是对顶角,
∴∠AOC=∠BOD=52°,
∴∠AOF=∠COF-∠AOC=90°-52°=38°;
(2)相等,
理由:∵∠AOC与∠BOD是对顶角,
∴∠AOC=∠BOD=52°,
∵OE是∠AOC的平分线,
∴∠AOE=$\frac{1}{2}$∠AOC=26°,
又∵OG⊥OE,
∴∠EOG=90°,
∴∠BOG=180°-∠AOE-∠EOG=64°,
而∠EOF=∠AOF+∠AOE=38°+26°=64°,
∴∠EOF=∠BOG.
点评 此题主要考查了垂线的定义以及角平分线的定义和对顶角定义,正确把握相关定义是解题关键.

练习册系列答案
相关题目
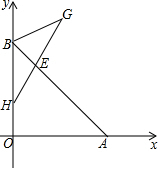 如图,点B(0,b),点A(a,0)分别在y轴、x轴正半轴上,且满足
如图,点B(0,b),点A(a,0)分别在y轴、x轴正半轴上,且满足