题目内容
5.某小组计划做一批“中华结”.如果每人做6个,那么比计划多了8个;如果每人做4个,那么比计划少了42个.
请你根据以上信息,提出一个用一元一次方程解决的问题,并写出解答过程.
分析 首先提出问题:这批“中华结”的个数是多少?设该批“中华结”的个数为x个,根据加工总个数=单人加工个数×人数结合该小组人数不变找出关于x的一元一次方程,解之即可得出结论.
解答 解:这批“中华结”的个数是多少?
设该批“中华结”的个数为x个,
根据题意得:$\frac{x+8}{6}$=$\frac{x-42}{4}$,
解得:x=142.
答:这批“中华结”的个数为142个.
点评 本题考查了一元一次方程的应用,根据加工总个数=单人加工个数×人数结合该小组人数不变列出关于x的一元一次方程是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
13.苏轼在《冬景》中赞美柑橘,“…一年好景君须记,最是橙黄橘绿时.”柑橘是秋冬季节非常时令的水果.但是柑橘在运输、储存中会有损坏,公司必须估算出可能损坏的柑橘总数,以便将损坏的柑橘的成本折算到没有损坏的柑橘的售价中.销售人员首先从所有的柑橘中随机抽取若干柑橘,进行柑橘损坏率的统计,并把获得的数据记录在下表中.估计一下柑橘损坏的概率是0.1 (结果保留小数点后一位).
| 柑橘总质量n/Kg | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
| 损坏柑橘质量m/Kg | 5.50 | 10.50 | 15.15 | 19.42 | 24.25 | 30.93 | 35.32 | 39.24 | 44.57 | 51.51 |
| 柑橘损坏的频率$\frac{m}{n}$ (结果保留小数点后三位) | 0.110 | 0.105 | 0.101 | 0.097 | 0.097 | 0.103 | 0.101 | 0.098 | 0.099 | 0.103 |
17.若一次函数y=(2-m)x-4的图象经过点A(x1,y1)和点B(x2,y2),当x1<x2时,y1>y2,则m的取值范围是( )
| A. | m<2 | B. | m>2 | C. | m≤2 | D. | m≥2 |
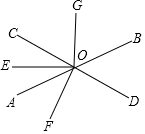 如图,直线AB与CD相交于O,OE是∠AOC的平分线,OF⊥CD,OG⊥OE,∠BOD=52°.
如图,直线AB与CD相交于O,OE是∠AOC的平分线,OF⊥CD,OG⊥OE,∠BOD=52°.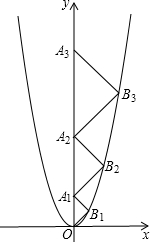 如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在y轴的正半轴上,点B1,B2,B3,…,Bn在二次函数y=x2位于第一象限的图象上,若△OB1A1,△A1B2A2,△A2B3A3,…,△An-1BnAn都是等腰直角三角形,其中∠B1=∠B2=∠B3=…=∠Bn=90°,则:
如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在y轴的正半轴上,点B1,B2,B3,…,Bn在二次函数y=x2位于第一象限的图象上,若△OB1A1,△A1B2A2,△A2B3A3,…,△An-1BnAn都是等腰直角三角形,其中∠B1=∠B2=∠B3=…=∠Bn=90°,则: 如图,等腰直角三角形ABC中,AB=4cm.点D是BC边上的动点,以AD为直角边作等腰直角三角形ADE.在点D从点B移动至点C的过程中,点E移动的路线长为4$\sqrt{2}$cm.
如图,等腰直角三角形ABC中,AB=4cm.点D是BC边上的动点,以AD为直角边作等腰直角三角形ADE.在点D从点B移动至点C的过程中,点E移动的路线长为4$\sqrt{2}$cm. 如图,拟从点A修建一条小径到边BC,若要使修建小径使用的材料最少,则过点A作AD⊥BC于点D,线段AD即为所求小径的位置,这样画的理由是垂线段最短.
如图,拟从点A修建一条小径到边BC,若要使修建小径使用的材料最少,则过点A作AD⊥BC于点D,线段AD即为所求小径的位置,这样画的理由是垂线段最短.