题目内容
5.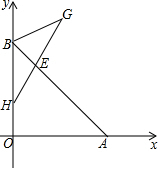 如图,点B(0,b),点A(a,0)分别在y轴、x轴正半轴上,且满足
如图,点B(0,b),点A(a,0)分别在y轴、x轴正半轴上,且满足$\sqrt{a-b}$+(b2-16)2=0.
(1)求A、B两点的坐标,∠OAB的度数;
(2)如图1,已知H(0,1),在第一象限内存在点G,HG交AB于E,使BE为△BHG的中线,且S△BHE=3,求点E到BH的距离.
分析 (1)根据非负数的性质可求得a、b的值,则可求得A、B两点的坐标,则可求得OA=OB,可求得∠OAB;
(2)由H、B的坐标可求得BH,利用△BHE的面积可求得点E到BH的距离.
解答 解:
(1)∵$\sqrt{a-b}$+(b2-16)2=0,
∴b2-16=0,且a-b=0,
∵点B(0,b),点A(a,0)分别在y轴、x轴正半轴上,
∴b>0,
∴a=b=4,
∴A(4,0),B(0,4),
∴OA=OB=4,
∴∠OAB=45°;
(2)∵H(0,1),
∴BH=4-1=3,
设点E到BH的距离为h,则S△BHE=$\frac{1}{2}$BH•h,
∴$\frac{1}{2}$×3h=3,解得h=2,
即点E到BH的距离为2.
点评 本题主要考查非负数的性质及三角形的面积,在(1)中利用非负数的性质求得a、b的值是解题的关键,在(2)中利用三角形的面积公式得到关于h的方程是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
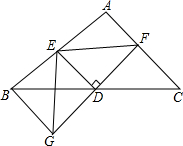 如图,△ABC中,D是BC的中点,过D点的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥GF交AB于点E,连接EG.
如图,△ABC中,D是BC的中点,过D点的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥GF交AB于点E,连接EG. 如图,在等腰直角△ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.
如图,在等腰直角△ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.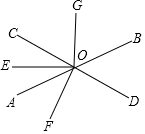 如图,直线AB与CD相交于O,OE是∠AOC的平分线,OF⊥CD,OG⊥OE,∠BOD=52°.
如图,直线AB与CD相交于O,OE是∠AOC的平分线,OF⊥CD,OG⊥OE,∠BOD=52°.