题目内容
如图，长方体的高为8cm，底面是正方形，边长为3cm，现有绳子从A出发，沿长方体表面到达C处，则绳子的最短长度是（ ）| A、8 | B、9 | C、10 | D、11 |
考点：平面展开-最短路径问题
专题：
分析：把长方体右边的表面展开，连接AC，则AC就是绳子的最短时经过的路径，然后根据勾股定理求解．
解答：
解：如图所示，将长方体右边的表面翻折90°（展开），
连接AC，显然两点之间线段最短，AC为点A到点C的最短距离，
由勾股定理知：AC2=82+（3+3）2=100，AC=10cm．
即绳子最短为10cm．
故选：C．
解：如图所示，将长方体右边的表面翻折90°（展开），连接AC，显然两点之间线段最短，AC为点A到点C的最短距离，
由勾股定理知：AC2=82+（3+3）2=100，AC=10cm．
即绳子最短为10cm．
故选：C．
点评：本题是勾股定理的应用，还利用了两点之间线段最短的性质．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
矩形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图所示放置．点A1，A2，A3，A4…和点C1，C2，C3，C4…，分别在直线y=kx+b（k＞0）和x轴上，若点B1（1，2），B2（3，4），且满足若关于x的不等式kx2+（k-6）x+2＞0的解为全体实数，则实数k的取值范围是（ ）
| A、-2＜k＜18 |
| B、-18＜k＜-2 |
| C、2＜k＜18 |
| D、-18＜k＜2 |
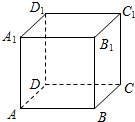如图，设正方体ABCD-A1B1C1D1的棱长为1，黑、白两个甲壳虫同时从A点出发，以相同的速度分别沿棱向前爬行，黑甲壳虫爬行的路线是AA1→A1D1→…，白甲壳虫爬行的路线是AB→BB1→…，并且都遵循如下规则：所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交（其中n是正整数）．那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时，它们之间的距离是（ ）下列式子中，是二次根式的是（ ）
A、
| |||
B、
| |||
C、
| |||
| D、-5 |
将矩形ABCD沿BE折叠，得到如图所示的图形，已知∠CBA′=34°，则∠AEB的大小是（ ）| A、34° | B、56° |
| C、28° | D、62° |
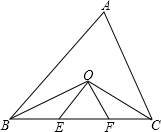如图，△ABC的角平分线BO、CO交于点O，OE∥AB，OF∥AC，BC=10，①△OEF的周长=