题目内容
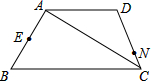 如图,已知等腰梯形ABCD,AD∥BC,AB⊥AC,AB=AD=DC=4cm,点N在DC上,且CN=1cm,E是AB中点,请在对角线AC上找一点M使EM+MN的值最小,并求出EM+MN的最小值.
如图,已知等腰梯形ABCD,AD∥BC,AB⊥AC,AB=AD=DC=4cm,点N在DC上,且CN=1cm,E是AB中点,请在对角线AC上找一点M使EM+MN的值最小,并求出EM+MN的最小值.考点:轴对称-最短路线问题,等腰梯形的性质
专题:
分析:首先得出梯形底角的度数,进而连接EN即可确定M的位置,连接EN,交AC于M,作EH⊥BC于H,NF⊥BC于F,作NG⊥EH于G,通过解直角三角形求得EH、BH、FC、NF的值,进而求得GN、EG的值根据勾股定理就可求出其和最小值.
解答: 解:连接EN,交AC于M,作EH⊥BC于H,NF⊥BC于F,作NG⊥EH于G,
解:连接EN,交AC于M,作EH⊥BC于H,NF⊥BC于F,作NG⊥EH于G,
∵四边形ABCD是等腰梯形,AD∥BC,AB⊥AC,AB=AD=DC=4cm,
∴∠B=∠DCB,∠DAC=∠DCA,∠DAC=∠ACB,
∴设∠ACB=x,则∠B=2x,
∴3x=90°,
解得:x=30°,
∴∠ACB=30°,
∴BC=2AB=8cm,
∵E是AB的中点,
∴EB=2cm,
∴BH=
BE=1,EH=
BE=
,
∵NC=1,
同理可证:FC=
,FN=
,
∴GN=HF=BC-BH-FC=8-1-
=
,EG=EH-NF=
,
∴EN=
=
,
∴EM+MN的最小值为
.
 解:连接EN,交AC于M,作EH⊥BC于H,NF⊥BC于F,作NG⊥EH于G,
解:连接EN,交AC于M,作EH⊥BC于H,NF⊥BC于F,作NG⊥EH于G,∵四边形ABCD是等腰梯形,AD∥BC,AB⊥AC,AB=AD=DC=4cm,
∴∠B=∠DCB,∠DAC=∠DCA,∠DAC=∠ACB,
∴设∠ACB=x,则∠B=2x,
∴3x=90°,
解得:x=30°,
∴∠ACB=30°,
∴BC=2AB=8cm,
∵E是AB的中点,
∴EB=2cm,
∴BH=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∵NC=1,
同理可证:FC=
| 1 |
| 2 |
| ||
| 2 |
∴GN=HF=BC-BH-FC=8-1-
| 1 |
| 2 |
| 13 |
| 2 |
| ||
| 2 |
∴EN=
| EG2+GN2 |
| 43 |
∴EM+MN的最小值为
| 43 |
点评:此题主要考查了轴对称求最短路线以及等腰梯形的性质等知识,解决此题的关键是确定点M的位置.如果在直线的异侧有两个点,要在直线上找一点到两个点的距离之和最短,方法是连接这两个点与直线的交点即为到两个点的距离之和最小的点的位置.

练习册系列答案
相关题目
 如图,菱形ABCD周长为16,∠ADC=120°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是
如图,菱形ABCD周长为16,∠ADC=120°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是 如图,AF∥BC,点D是AF上一点,BF与CD交于点E,点E是CD的中点.
如图,AF∥BC,点D是AF上一点,BF与CD交于点E,点E是CD的中点.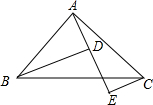 如图所示,A,D,E三点在同一直线上,且△BAD≌△ACE.
如图所示,A,D,E三点在同一直线上,且△BAD≌△ACE.