题目内容
6. 已知:如图所示,⊙O中,△ABC为内接三角形,AD是⊙O的直径.CE⊥AD于E,CE的延长线交AB于F,求证:AC2=AF•AB.
已知:如图所示,⊙O中,△ABC为内接三角形,AD是⊙O的直径.CE⊥AD于E,CE的延长线交AB于F,求证:AC2=AF•AB.
分析 因为直径所对的圆周角是直角,所以作辅助线:连接CD;利用同角的余角相等,可得∠ACF=∠D,又由同弧所对的圆周角相等,可得∠B=∠D,证得∠B=∠ACF,又因为∠CAB是公共角,即可证得△ACF∽△ABC;由相似三角形的对应边成比例,即可证得AC2=AF•AB.
解答 证明:连接CD,
∵AD是⊙O的直径,
∴∠ACD=90°,
∴∠ACF+∠DCF=90°,
∵CF⊥AD,
∴∠D+∠DCF=90°,
∴∠ACF=∠D,
∵∠B=∠D,
∴∠B=∠ACF,
∵∠CAF=∠BAC,
∴△ACF∽△ABC,
∴AC:AB=AF:AC,
∴AC2=AF•AB.
点评 此题考查了相似三角形的判定与性质与圆的性质.解此题的关键是掌握辅助线的作法,在圆中,构造直径所对的角是直角是常见辅助线,同学们应注意掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.已知反比例函数y=$\frac{m+1}{x}$,在每一象限内,y随x的增大而减小,则m的取值范围是( )
| A. | m<0 | B. | m<-1 | C. | m>1 | D. | m>-1 |
17.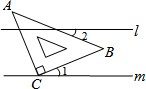 如图,直线l∥m,将含有45°角的三角形板ABC的直角顶点C放在直线m上,若∠1=20°,则∠2的度数为( )
如图,直线l∥m,将含有45°角的三角形板ABC的直角顶点C放在直线m上,若∠1=20°,则∠2的度数为( )
 如图,直线l∥m,将含有45°角的三角形板ABC的直角顶点C放在直线m上,若∠1=20°,则∠2的度数为( )
如图,直线l∥m,将含有45°角的三角形板ABC的直角顶点C放在直线m上,若∠1=20°,则∠2的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
16.下列运算正确的是( )
| A. | (2a2)3=6a6 | B. | -a2b2•3ab3=-3a2b5 | ||
| C. | $\frac{b}{a-b}$+$\frac{a}{b-a}$=-1 | D. | $\frac{{a}^{2}-1}{a}$•$\frac{1}{a+1}$=-1 |
 如图,在平行四边形ABCD中,E为AD的中点,连接BE交AC于点F.已知△ABE的面积为4,则△ABC的面积为8.
如图,在平行四边形ABCD中,E为AD的中点,连接BE交AC于点F.已知△ABE的面积为4,则△ABC的面积为8.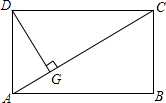 如图,在矩形ABCD中,DG⊥AC,垂足为G.
如图,在矩形ABCD中,DG⊥AC,垂足为G.