题目内容
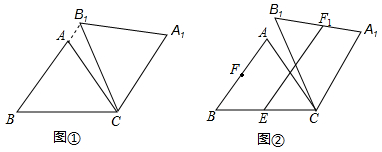
15.在△ABC中,AB=AC=5,cos∠ABC=$\frac{3}{5}$,将△ABC绕点C顺时针旋转,得到△A1B1C.(1)如图①,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;
(2)如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1,求线段EF1长度的最大值与最小值的差.
分析 (1)①根据旋转的性质和平行线的性质证明;
②过A作AF⊥BC于F,过C作CE⊥AB于E,根据三角函数和三角形的面积公式解答;
(2)过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,和以C为圆心BC为半径画圆交BC的延长线于F1,得出最大和最小值解答即可.
解答 解:(1)①证明:∵AB=AC,B1C=BC,
∴∠AB1C=∠B,∠B=∠ACB,
∵∠AB1C=∠ACB(旋转角相等),
∴∠B1CA1=∠AB1C,
∴BB1∥CA1;
②过A作AF⊥BC于F,过C作CE⊥AB于E,如图①: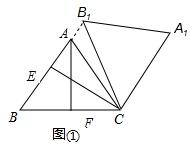
∵AB=AC,AF⊥BC,
∴BF=CF,
∵cos∠ABC=$\frac{3}{5}$,AB=5,
∴BF=3,
∴BC=6,
∴B1C=BC=6,
∵CE⊥AB,
∴BE=B1E=$\frac{3}{5}×6=\frac{18}{5}$,
∴BB1=$\frac{36}{5}$,CE=$\frac{4}{5}×6=\frac{24}{5}$,
∴AB1=$\frac{36}{5}-5=\frac{11}{5}$,
∴△AB1C的面积为:$\frac{1}{2}×\frac{11}{5}×\frac{24}{5}=\frac{132}{25}$;
(2)如图2,过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,EF1有最小值,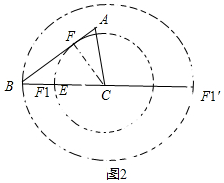
此时在Rt△BFC中,CF=$\frac{24}{5}$,
∴CF1=$\frac{24}{5}$,
∴EF1的最小值为$\frac{24}{5}-3=\frac{9}{5}$;
如图,以C为圆心BC为半径画圆交BC的延长线于F1,EF1有最大值;
此时EF1=EC+CF1=3+6=9,
∴线段EF1的最大值与最小值的差为$9-\frac{9}{5}=\frac{36}{5}$.
点评 此题考查几何变换问题,关键是根据旋转的性质和三角形的面积公式进行解答.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 如图是某校学生参加课外兴趣小组的人数占总人数比例的统计图,则参加人数最多的课外兴趣小组是( )
如图是某校学生参加课外兴趣小组的人数占总人数比例的统计图,则参加人数最多的课外兴趣小组是( )| A. | 音乐组 | B. | 美术组 | C. | 体育组 | D. | 科技组 |
 已知:如图所示,⊙O中,△ABC为内接三角形,AD是⊙O的直径.CE⊥AD于E,CE的延长线交AB于F,求证:AC2=AF•AB.
已知:如图所示,⊙O中,△ABC为内接三角形,AD是⊙O的直径.CE⊥AD于E,CE的延长线交AB于F,求证:AC2=AF•AB.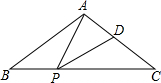 如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.