题目内容
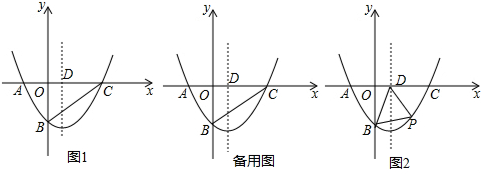
11. 如图,在矩形ABCD中,DG⊥AC,垂足为G.
如图,在矩形ABCD中,DG⊥AC,垂足为G.(1)△ADG与△ACD、△CDG与△CAD相似吗?为什么?
(2)若AG=6,CG=12,求矩形ABCD的面积.
分析 (1)运用有两对对应角的三角形相似可得证;
(2)运用(1)中的三角形相似得比例中项:AD2=AG•AC,CD2=CG•AC,求出矩形的长和宽,进而求出矩形的面积.
解答 解:(1)△ADG∽△ACD、△CDG∽△CAD;
∵四边形ABCD是矩形,
∴∠ADC=90°,
∵DG⊥AC,
∴∠AGD=∠DGC=90°,
∴∠ADC=∠AGD,
又∠A=∠A ,
,
∴△ADG∽△ACD,
同理可得:△CDG∽△CAD;
(2)∵△ADG∽△ACD,
∴AD2=AG•AC,
∵△CDG∽△CAD,
∴CD2=CG•AC,
∵AG=6,CG=12,
∴AC=18,
∴AD=6$\sqrt{3}$,CD=6$\sqrt{6}$,
∴S矩形ABCD=AD×CD=6$\sqrt{3}$×6$\sqrt{6}$=108$\sqrt{2}$.
点评 本题考查了相似三角形的判定与性质以及面积的计算,建立数学模型,熟悉此图形中的比例中项是解决此类问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.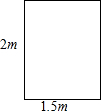 如图,是一扇高为2m,宽为1.5m的门框,现有3块薄木板,尺寸如下:①号木板长3m,宽
如图,是一扇高为2m,宽为1.5m的门框,现有3块薄木板,尺寸如下:①号木板长3m,宽
2.7m;②号木板长4m,宽2.4m;③号木板长2.8m,宽2.8m.可以从这扇门通过的木板是
( )
 如图,是一扇高为2m,宽为1.5m的门框,现有3块薄木板,尺寸如下:①号木板长3m,宽
如图,是一扇高为2m,宽为1.5m的门框,现有3块薄木板,尺寸如下:①号木板长3m,宽2.7m;②号木板长4m,宽2.4m;③号木板长2.8m,宽2.8m.可以从这扇门通过的木板是
( )
| A. | ①号 | B. | ②号 | C. | ③号 | D. | 均不能通过 |
16.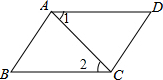 如图所示,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( )
如图所示,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( )
 如图所示,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( )
如图所示,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( )| A. | AB=DC | B. | ∠1=∠2 | C. | AB=AD | D. | ∠D=∠B |
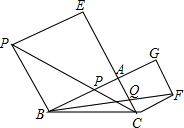 如图,在△ABC中,∠BAC=90°,分别以AB,AC为边向外作正方形ABDE和ACFG,连接DC,FB,分别交AB,AC于P,Q.求证:AP=AQ.
如图,在△ABC中,∠BAC=90°,分别以AB,AC为边向外作正方形ABDE和ACFG,连接DC,FB,分别交AB,AC于P,Q.求证:AP=AQ. 已知:如图所示,⊙O中,△ABC为内接三角形,AD是⊙O的直径.CE⊥AD于E,CE的延长线交AB于F,求证:AC2=AF•AB.
已知:如图所示,⊙O中,△ABC为内接三角形,AD是⊙O的直径.CE⊥AD于E,CE的延长线交AB于F,求证:AC2=AF•AB.