题目内容
1.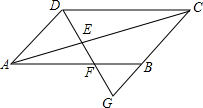 如图,?ABCD中,过D的直线交AC,AB及CB的延长线于E,F,G.
如图,?ABCD中,过D的直线交AC,AB及CB的延长线于E,F,G.求证:DE2=EF•EG.
分析 由平行四边形的性质得出AB∥CD,AD∥BC,证出△CDE∽△AFE,△CGE∽△ADE,得出对应边成比例,得出$\frac{DE}{EF}=\frac{EG}{DE}$,即可得出结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴△CDE∽△AFE,△CGE∽△ADE,
∴$\frac{DE}{EF}=\frac{CE}{AE}$,$\frac{EG}{DE}=\frac{CE}{AE}$,
∴$\frac{DE}{EF}=\frac{EG}{DE}$,
∴DE2=EF•EG.
点评 本题考查了平行四边形的性质、相似三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形相似得出比例式是解决问题的关键.

练习册系列答案
相关题目
16.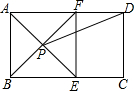 如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.
如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.
(1)求证:四边形ABEF是正方形;
(2)如果AB=4,AD=7,求tan∠ADP的值.
 如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.
如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.(1)求证:四边形ABEF是正方形;
(2)如果AB=4,AD=7,求tan∠ADP的值.
9.设a=$\sqrt{2}-1$,b=$\sqrt{5}$-2,c=$\sqrt{10}$-3.则a、b、c的大小关系为( )
| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | c<b<a |
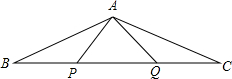 如图,P,Q是△ABC的边BC上的两点,且BP=QC=AP=AQ.
如图,P,Q是△ABC的边BC上的两点,且BP=QC=AP=AQ.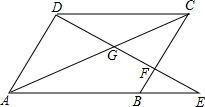 如图,四边形ABCD为平行四边形,试说明:
如图,四边形ABCD为平行四边形,试说明: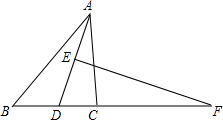 如图,在△ABC中,AD的垂直平分线交AD于E,交BC的延长线于F,FD2=FB•FC,求证:AD平分△BAC.
如图,在△ABC中,AD的垂直平分线交AD于E,交BC的延长线于F,FD2=FB•FC,求证:AD平分△BAC.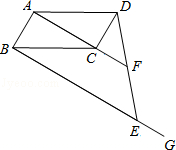 如图,在平行四边形ABCD中,过点B作BE∥AC,在BG上取点E,连接DE交AC的延长线于点F.
如图,在平行四边形ABCD中,过点B作BE∥AC,在BG上取点E,连接DE交AC的延长线于点F.