题目内容
若直线y=2x-3与直线y=x-k+1的交点在第三象限,则k的取值范围是 .
考点:两条直线相交或平行问题
专题:计算题
分析:根据两直线相交的问题,通过解方程组得到两直线的交点坐标为(-k+4,-2k+5),然后根据第三象限点的坐标特征得到-k+4<0且-2k+5<0,再解不等式组即可.
解答:解:解方程组
得
,
所以两直线的交点坐标为(-k+4,-2k+5),
因为点(-k+4,-2k+5)在第三象限,
所以-k+4<0且-2k+5<0,
所以k的取值范围为k>4.
故答案为k>4.
|
|
所以两直线的交点坐标为(-k+4,-2k+5),
因为点(-k+4,-2k+5)在第三象限,
所以-k+4<0且-2k+5<0,
所以k的取值范围为k>4.
故答案为k>4.
点评:本题考查了两条直线相交或平行的问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么它们的自变量系数相同,即k值相同.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
抛物线y=-2x2-4x-5经过平移得到y=-2x2,平移方法是( )
| A、向左平移1个单位,再向下平移3个单位 |
| B、向左平移1个单位,再向上平移3个单位 |
| C、向右平移1个单位,再向下平移3个单位 |
| D、向右平移1个单位,再向上平移3个单位 |
若A(-3.5,y1),B(-1,y2),C(1,y2)为二次函数y=-x2-4x+5的图象上的三点,则y1,y2,y3的大小关系是( )
| A、y1<y2<y3 |
| B、y2<y3<y1 |
| C、y2<y1<y3 |
| D、y3<y1<y2 |
下列各式不是同类项的是( )
| A、a2b与3a2b | ||
| B、x与2x | ||
C、
| ||
D、
|
 已知在平面直角坐标系xOy中,二次函数y=ax2+bx的图象经过点(1,-3)和点(-1,5);
已知在平面直角坐标系xOy中,二次函数y=ax2+bx的图象经过点(1,-3)和点(-1,5);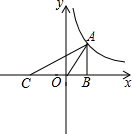 如图,直线AC:y=x+k与双曲线y=
如图,直线AC:y=x+k与双曲线y= 如图,A、B两个带指针的转盘分别被分成三个面积相等的扇形,转盘A上的数字分别是2,5,9,转盘B上的数字分别是3,4,8(两个转盘除表面数字不同外,其他完全相同).分别转动A盘、B盘各一次,转动过程中,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.
如图,A、B两个带指针的转盘分别被分成三个面积相等的扇形,转盘A上的数字分别是2,5,9,转盘B上的数字分别是3,4,8(两个转盘除表面数字不同外,其他完全相同).分别转动A盘、B盘各一次,转动过程中,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.