题目内容
20.探究题:(1)小明和小亮在计算这样一道求值题:“当a=-3时,求整式7a2-[5a-(4a-1)+4a2]-(2a2-a+1)的值.”小亮正确求得结果为7,而小明在计算时,错把a=-3看成a=3,但计算结果也是正确的.你能说明为什么吗?
(2)小张买了张50元的乘车IC卡,如果他乘车的次数用m表示,则记录他每次乘车后的余额n(元)如下表:
| 次数m | 余额n(元) |
| 1 | 50-0.8 |
| 2 | 50-1.6 |
| 3 | 50-2.4 |
| 4 | 50-3.2 |
| … | … |
②利用上述关系式计算小张乘了13次车后还剩下多少元?小张最多能乘多少次车?
(3)观察如下计算:
$\sqrt{4}$×$\sqrt{9}$=6,$\sqrt{4×9}$=6
$\sqrt{16}$×$\sqrt{25}$=20,$\sqrt{16×25}$=20;
$\sqrt{\frac{1}{121}}$×$\sqrt{36}$=$\frac{6}{11}$,$\sqrt{\frac{1}{121}×36}$=$\frac{6}{11}$
你能找出规律吗?请按找到的规律计算:
①$\sqrt{5}$×$\sqrt{20}$
②$\sqrt{1\frac{2}{3}}$×$\sqrt{9\frac{3}{5}}$.
分析 (1)原式去括号合并得到最简结果,即可作出判断;
(2)①归纳总结得到一般性规律,确定出所求关系式即可;
②令m=13求出n的值,确定出余的钱数,令n=0,求出m的值,确定出最多乘车的次数即可;
(3)写出得出的规律,利用得出的规律确定出所求即可.
解答 解:(1)原式=7a2-5a+4a-1-4a2-2a2+a-1=a2-2,
当a=3或-3时,原式=9-2=7;
(2)①n=50-0.8m(m≥1,且m为正整数);
②当m=13时,n=39.6元,
令n=0,得到50-0.8m=0,
解得:m=62.5,
取整数值为62,
则小张乘了13次车后还剩下39.6元,小张最多能乘62次车;
(3)规律为$\sqrt{a}$•$\sqrt{b}$=$\sqrt{ab}$,
①原式=$\sqrt{5×20}$=10;
②原式=$\sqrt{\frac{5}{3}×\frac{48}{5}}$=4.
点评 此题考查了整式的混合运算,实数的运算,弄清题中的规律是解本题的关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
9.在二次函数y=x2-2x+3的图象中,若y随x的增大而增大,则x的取值范围是( )
| A. | x<-1 | B. | x>-1 | C. | x<1 | D. | x>1 |
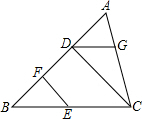 已知:如图,CD⊥AB,EF⊥AB,垂足分别是D,F,∠BEF=∠CDG,试说明:∠B+∠BDG=180°.
已知:如图,CD⊥AB,EF⊥AB,垂足分别是D,F,∠BEF=∠CDG,试说明:∠B+∠BDG=180°.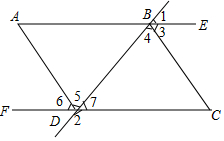 如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠FDB,试问∠3与∠4有怎样的数量关系,并说明理由.
如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠FDB,试问∠3与∠4有怎样的数量关系,并说明理由.