题目内容
15.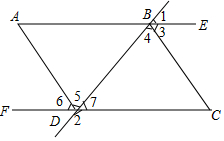 如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠FDB,试问∠3与∠4有怎样的数量关系,并说明理由.
如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠FDB,试问∠3与∠4有怎样的数量关系,并说明理由.
分析 根据角平分线定义得出∠5=∠6,根据∠1+∠2=180°求出∠ABD+∠FDB=180°,根据平行线的判定得出AB∥CD,根据平行线的性质得出∠A=∠6,求出∠6=∠C,根据平行线的判定得出AD∥BC,根据平行线的性质得出∠4=∠5,∠3=∠C,即可求出答案.
解答 解:∠3=∠4,
理由是:∵DA平分∠FDB,
∴∠5=∠6,
∵∠1+∠2=180°,∠1=∠ABD,∠2=∠FDB,
∴∠ABD+∠FDB=180°,
∴AB∥CD,
∴∠A=∠6,
∵∠A=∠C,
∴∠6=∠C,
∴AD∥BC,
∴∠4=∠5,
∵AB∥CD,
∴∠3=∠C,
∵∠5=∠6,∠6=∠C,
∴∠3=∠4.
点评 本题考查了平行线的性质和判定,能灵活运用定理进行推理是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
10.下列关于因式分解的情况正确的是( )
| A. | 4x2y+xy+3xy2=xy(4x+3y) | B. | $\frac{1}{4}$a2+ab+b2=$\frac{1}{4}$(a+2b)2 | ||
| C. | m2+4=(m+2)2 | D. | 若x2-x+42=(x+a)(x+b),则a,b异号 |
20.探究题:
(1)小明和小亮在计算这样一道求值题:“当a=-3时,求整式7a2-[5a-(4a-1)+4a2]-(2a2-a+1)的值.”小亮正确求得结果为7,而小明在计算时,错把a=-3看成a=3,但计算结果也是正确的.你能说明为什么吗?
(2)小张买了张50元的乘车IC卡,如果他乘车的次数用m表示,则记录他每次乘车后的余额n(元)如下表:
①写出乘车的次数m表示余额n(元)的关系式;
②利用上述关系式计算小张乘了13次车后还剩下多少元?小张最多能乘多少次车?
(3)观察如下计算:
$\sqrt{4}$×$\sqrt{9}$=6,$\sqrt{4×9}$=6
$\sqrt{16}$×$\sqrt{25}$=20,$\sqrt{16×25}$=20;
$\sqrt{\frac{1}{121}}$×$\sqrt{36}$=$\frac{6}{11}$,$\sqrt{\frac{1}{121}×36}$=$\frac{6}{11}$
你能找出规律吗?请按找到的规律计算:
①$\sqrt{5}$×$\sqrt{20}$
②$\sqrt{1\frac{2}{3}}$×$\sqrt{9\frac{3}{5}}$.
(1)小明和小亮在计算这样一道求值题:“当a=-3时,求整式7a2-[5a-(4a-1)+4a2]-(2a2-a+1)的值.”小亮正确求得结果为7,而小明在计算时,错把a=-3看成a=3,但计算结果也是正确的.你能说明为什么吗?
(2)小张买了张50元的乘车IC卡,如果他乘车的次数用m表示,则记录他每次乘车后的余额n(元)如下表:
| 次数m | 余额n(元) |
| 1 | 50-0.8 |
| 2 | 50-1.6 |
| 3 | 50-2.4 |
| 4 | 50-3.2 |
| … | … |
②利用上述关系式计算小张乘了13次车后还剩下多少元?小张最多能乘多少次车?
(3)观察如下计算:
$\sqrt{4}$×$\sqrt{9}$=6,$\sqrt{4×9}$=6
$\sqrt{16}$×$\sqrt{25}$=20,$\sqrt{16×25}$=20;
$\sqrt{\frac{1}{121}}$×$\sqrt{36}$=$\frac{6}{11}$,$\sqrt{\frac{1}{121}×36}$=$\frac{6}{11}$
你能找出规律吗?请按找到的规律计算:
①$\sqrt{5}$×$\sqrt{20}$
②$\sqrt{1\frac{2}{3}}$×$\sqrt{9\frac{3}{5}}$.
7.下列说法正确的是( )
| A. | (-3)2的算术平方根是3 | B. | $\sqrt{225}$的平方根是±15 | ||
| C. | 当x=0或2时,x$\sqrt{x-2}$=0 | D. | $\frac{\sqrt{3}}{2}$是分数 |
5.下列调查中,最适合采用普查方式的是( )
| A. | 调查2017年春节晚会的收视率 | |
| B. | 调查宝应湖中鱼的种类和数量 | |
| C. | 调查某品牌节能灯的使用寿命 | |
| D. | 调查某航班的旅客是否携带了违禁物品 |
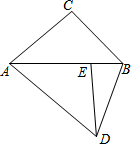 如图,将△ABC绕点A顺时针旋转,使点C落在边AB上的点E处,点B落在点D处,连结BD,如果∠DAC=∠DBA,那么∠BAC度数是36度.
如图,将△ABC绕点A顺时针旋转,使点C落在边AB上的点E处,点B落在点D处,连结BD,如果∠DAC=∠DBA,那么∠BAC度数是36度.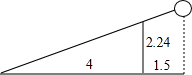 已知女排赛场标准球网的高度是2.24米,在2016年奥运会女排比赛中,某队球员在一次扣球时,球恰好擦网而过(击球擦网落地过程为直线),落在对方场地距离球网4米的位置上,此时该运动员距离球网1.5米,则该运动员击球的高度是3.08米.
已知女排赛场标准球网的高度是2.24米,在2016年奥运会女排比赛中,某队球员在一次扣球时,球恰好擦网而过(击球擦网落地过程为直线),落在对方场地距离球网4米的位置上,此时该运动员距离球网1.5米,则该运动员击球的高度是3.08米.