题目内容
17.已知y-1与x+1成正比例关系.(1)如果正比例系数为2,试用x表示y;
(2)若比例系数为k,且函数的图象与坐标轴围成的三角形面积为2,求k的值.
分析 (1)根据正比例函数y=kx的定义条件:k为常数且k≠0,自变量次数为1,列出表达式,化简即可得出答案.
(2)首先根据题意列出表达式,分别求出交点点的坐标,再根据面积公式列出等式,即可求得.
解答 解:(1)由题意可得:y-1=2(x+1),
化简得:y=2x+3.
(2)由题意可得:y-1=k(x+1),
∴y=kx+k+1,
∴与坐标轴的交点为(-$\frac{k+1}{k}$,0),(0,k+1)
∵函数的图象与坐标轴围成的三角形面积为2,
∴$\frac{1}{2}$|-$\frac{k+1}{k}$|•|k+1|=2,
解得:k=±1.
点评 此题主要考查了待定系数法求一次函数解析式和一次函数图象上点的坐标特征,难度不大,注意基础概念的掌握.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
6.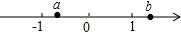 有理数a,b在数轴上对应点的位置如图所示,下列各式正确的是( )
有理数a,b在数轴上对应点的位置如图所示,下列各式正确的是( )
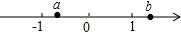 有理数a,b在数轴上对应点的位置如图所示,下列各式正确的是( )
有理数a,b在数轴上对应点的位置如图所示,下列各式正确的是( )| A. | a+b<0 | B. | a-b<0 | C. | a•b>0 | D. | $\frac{a}{b}$>0 |
 如图,在矩形ABCD中,点O是AC的中点,AC=2AB,延长AB至G,使BG=AB,连接GO交BC于点E,延长GO交AD于点F,判断四边形AECF的形状,并证明你的结论.
如图,在矩形ABCD中,点O是AC的中点,AC=2AB,延长AB至G,使BG=AB,连接GO交BC于点E,延长GO交AD于点F,判断四边形AECF的形状,并证明你的结论.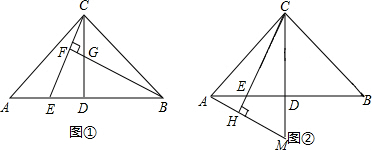
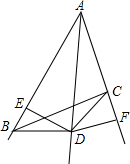 如图,AB>AC,已知点D是∠BAC的平分线上的点,过D作DE⊥AB于点E,作DF⊥AC于点F,∠ABD+∠ACD=180°.试着说明BD=DC.
如图,AB>AC,已知点D是∠BAC的平分线上的点,过D作DE⊥AB于点E,作DF⊥AC于点F,∠ABD+∠ACD=180°.试着说明BD=DC.