Question

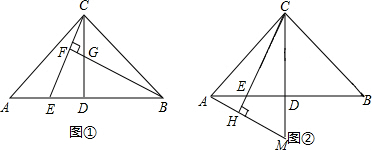
5．已知，在△ABC中，AC=BC，∠ACB=90°，点D是AB的中点，点E是AB边上一点．
（1）直线BF⊥CE于点F，交CD于点G（如图①），求证：AE=CG；
（2）直线AH⊥CE于点H，交CD的延长线于点M（如图②），找出图中与BE相等的线段，并证明．

Answer 1

分析 （1）先证出∠ACE=∠CBG，再由ASA证明△ACE≌△CBG，得出对应边相等即可；
（2）先证出∠CEB=∠CMA，再由AAS证明△BCE≌△ACM，得出对应边相等即可

解答 （1）证明：∵AC=BC，∠ACD=∠BCD=45°，
∴∠ACB=90°，
∴∠A=∠ABC=45°，∠ACE=90°-∠BCF，
∵BF⊥CE，
∴∠CFB=90°，
∴∠CBG=90°-∠BCF，
∴∠ACE=∠CBG，
在△ACE和△CBG中，
$\left\{\begin{array}{l}{∠A=∠BCG=45°}\\{AC=BC}\\{∠ACE=∠BCG}\end{array}\right.$，
∴△ACE≌△CBG（ASA），
∴AE=CG；
（2）解：CM=BE；理由：
∵CD⊥AB，AH⊥CE，
∴∠CDE=∠CHM=90°，
∴∠DCE+∠CEB=90°，∠DCE+∠CMA=90°，
∴∠CEB=∠CMA，
在△BCE和△ACM中，
$\left\{\begin{array}{l}{∠B=∠ACM=45°}\\{∠CEB=∠CMA}\\{AC=BC}\end{array}\right.$，
∴△BCE≌△ACM（AAS），
∴CM=BE．

点评 本题考查了全等三角形的判定与性质；熟练掌握全等三角形的判定方法是解决问题的关键．