题目内容
13.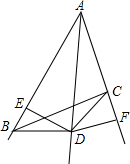 如图,AB>AC,已知点D是∠BAC的平分线上的点,过D作DE⊥AB于点E,作DF⊥AC于点F,∠ABD+∠ACD=180°.试着说明BD=DC.
如图,AB>AC,已知点D是∠BAC的平分线上的点,过D作DE⊥AB于点E,作DF⊥AC于点F,∠ABD+∠ACD=180°.试着说明BD=DC.
分析 由点D是∠BAC的平分线上的点,得到DE=DF,由∠ABD+∠ACD=180°得到∠ABD=∠DCF,从而推出△BDE≌△CDF,于是得到BD=DC.
解答 证明:∵点D是∠BAC的平分线上的点,过D作DE⊥AB于点E,作DF⊥AC于点F,
∴DE=DF,
∵∠ABD+∠ACD=180°,∠ACD+∠DCF=180°,
∴∠ABD=∠DCF,
在△BDE和△CDF中,
$\left\{\begin{array}{l}{∠BED=∠CFD}\\{∠ABD=∠DCF}\\{DE=DF}\end{array}\right.$,
∴△BDE≌△CDF,
∴BD=DC.
点评 本题主要考查了角的平分线的性质,全等三角形的判定与性质,熟练应用三角形全等的性质是解题的关键.

练习册系列答案
相关题目
 (1)分别化简$4\sqrt{\frac{1}{2}}$,$\frac{2}{5}\sqrt{125}$;
(1)分别化简$4\sqrt{\frac{1}{2}}$,$\frac{2}{5}\sqrt{125}$; 如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点D在AB上,AD=2cm.点E、F同时从点D出发,点E沿DA以1cm每秒的速度向点A运动,到达A点后立即以原速度沿AB向点B匀速运动;点F沿DB以2cm每秒的速度向点B匀速运动,点F运动到点B时停止,点E也随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧,设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠部分面积为S.
如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点D在AB上,AD=2cm.点E、F同时从点D出发,点E沿DA以1cm每秒的速度向点A运动,到达A点后立即以原速度沿AB向点B匀速运动;点F沿DB以2cm每秒的速度向点B匀速运动,点F运动到点B时停止,点E也随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧,设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠部分面积为S.