题目内容
10.分解因式:-3x2+27y2=-3(x+3y)(x-3y).分析 原式提取-3,再利用平方差公式分解即可.
解答 解:原式=-3(x2-9y2)
=-3(x+3y)(x-3y).
故答案为:-3(x+3y)(x-3y).
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
15.下列方程中,是一元二次方程的是( )
| A. | x2+x=x2-5 | B. | ${x^2}+\frac{2}{x}=4$ | C. | $\sqrt{{x^2}-4x}=6$ | D. | $\sqrt{2}{x^2}+5x-1=0$ |
2.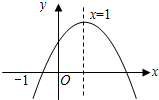 二次函数y=ax2+bx+c图所示,其中正确的结论是( )
二次函数y=ax2+bx+c图所示,其中正确的结论是( )
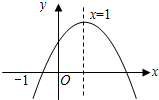 二次函数y=ax2+bx+c图所示,其中正确的结论是( )
二次函数y=ax2+bx+c图所示,其中正确的结论是( )| A. | b2-4ac<0 | B. | abc>0 | C. | 2a+b=0 | D. | a+b+c<0 |
17.已知∠1与∠2是邻补角,∠2是∠3的邻补角,那么∠1与∠3的关系是( )
| A. | 对顶角 | B. | 相等但不是对顶角 | ||
| C. | 邻补角 | D. | 互补但不是邻补角 |
 二次函数y=ax2+bx+c的图象如图所示,则b>0,b2-4ac>0,a-b+c<0.
二次函数y=ax2+bx+c的图象如图所示,则b>0,b2-4ac>0,a-b+c<0.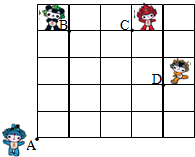 如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中,
如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中,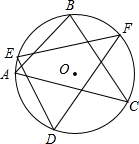 已知,如图,在⊙O中,AB=DE,BC=EF.求证:AC=DF.
已知,如图,在⊙O中,AB=DE,BC=EF.求证:AC=DF.