题目内容
5.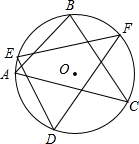 已知,如图,在⊙O中,AB=DE,BC=EF.求证:AC=DF.
已知,如图,在⊙O中,AB=DE,BC=EF.求证:AC=DF.
分析 由在⊙O中,AB=DE,BC=EF,根据弦与弧的关系,可得$\widehat{AB}$=$\widehat{DE}$,$\widehat{BC}$=$\widehat{EF}$,则可得$\widehat{AC}$=$\widehat{DF}$,继而证得结论.
解答 解:∵AB=DE,BC=EF,
∴$\widehat{AB}$=$\widehat{DE}$,$\widehat{BC}$=$\widehat{EF}$,
∴$\widehat{AC}$=$\widehat{DF}$,
∴AC=DF.
点评 此题考查了弧与弦的关系.注意在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.方程3x2-1=0的解为( )
| A. | ${x_1}=\frac{1}{3}$,${x_2}=-\frac{1}{3}$ | B. | ${x_1}=\frac{{\sqrt{3}}}{3}$,${x_2}=-\frac{{\sqrt{3}}}{3}$ | C. | ${x_1}={x_2}=\frac{1}{3}$ | D. | ${x_1}=\sqrt{3}$,${x_2}=-\sqrt{3}$ |
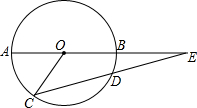 已知:如图,AB是⊙O的直径,CD是⊙O的弦,AB,CD的延长线交于E,若AB=2DE,∠C=40°,求∠E及∠AOC的度数.
已知:如图,AB是⊙O的直径,CD是⊙O的弦,AB,CD的延长线交于E,若AB=2DE,∠C=40°,求∠E及∠AOC的度数. ,则
,则 _________.
_________.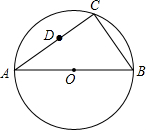 如图,AB为⊙O的直径,点C为⊙O上一动点,点D为弦AC的中点.
如图,AB为⊙O的直径,点C为⊙O上一动点,点D为弦AC的中点. 如图,AB∥CD,∠BAE=∠DCE=45°,则∠E=90°.
如图,AB∥CD,∠BAE=∠DCE=45°,则∠E=90°.