题目内容
1.不等式$\sqrt{2}$x-3<$\sqrt{3}$x的解集是x>-3$\sqrt{3}$-3$\sqrt{2}$.分析 利用不等式的基本性质,将不等式未知项和常数项各移到一边,解得x的解集.
解答 解:由$\sqrt{2}$x-3<$\sqrt{3}$x,得
$\sqrt{2}$x-$\sqrt{3}$x<3,
($\sqrt{2}$-$\sqrt{3}$)x<3,
x>$\frac{3}{\sqrt{2}-\sqrt{3}}$,即x>-3$\sqrt{3}$-3$\sqrt{2}$.
故答案是:x>-3$\sqrt{3}$-3$\sqrt{2}$.
点评 本题考查了二次根式的应用.解题的关键是熟悉不等式的基本性质:不等式的两边同时除以负数,不等号的方向发生改变.

练习册系列答案
相关题目
11.下列运算中结果正确的是( )
| A. | -3x+5x=-8x | B. | 5y-3y=2 | C. | 3x2y-2x2y=x2y | D. | 3a+2b=5ab |
16.化简$\sqrt{-x{y}^{2}}$(y<0)的结果是( )
| A. | y$\sqrt{x}$ | B. | y$\sqrt{-x}$ | C. | -y$\sqrt{x}$ | D. | -y$\sqrt{-x}$ |
13.已知线段MN=6cm,点P是线段MN的一个黄金分割点,则其中较长线段MP的长是( )cm.
| A. | 9-3$\sqrt{5}$ | B. | 3$\sqrt{5}$-3 | C. | 3$\sqrt{5}$-1 | D. | 3-$\sqrt{5}$ |
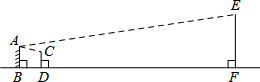 如图,小明在墙上挂了一面镜子AB,调整好标杆CD,正好通过标杆顶部在镜子上边缘A处看到旗杆的顶端E的影子,已知AB=2m,CD=1.5m,BD=2m,BF=20m,则旗杆EF的高度为7m.
如图,小明在墙上挂了一面镜子AB,调整好标杆CD,正好通过标杆顶部在镜子上边缘A处看到旗杆的顶端E的影子,已知AB=2m,CD=1.5m,BD=2m,BF=20m,则旗杆EF的高度为7m.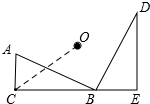 如图,将Rt△ABC绕O点旋转90°,得Rt△BDE,其中∠ACB=∠BED=90°,AC=6,AB=10,则点C与旋转中心点O的距离OC的长是7$\sqrt{2}$.
如图,将Rt△ABC绕O点旋转90°,得Rt△BDE,其中∠ACB=∠BED=90°,AC=6,AB=10,则点C与旋转中心点O的距离OC的长是7$\sqrt{2}$.