题目内容
10.如图1,在?ABCD中,E、F分别是AB、CD上的点,若CE∥AF.(1)求证:DE∥BF;
(2)如图2,在四边形ABCD中,AD∥BC,E、F分别是AB,CD上的点,若CE∥AF,求证:DE∥BF.
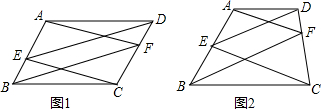
分析 (1)首先利用平行四边形的性质得出AD∥BC,AD=BC,进而得出四边形AECF是平行四边形,即可得出答案;
(2)延长AF,DE交BC的延长线于点N,M,根据平行线成比例线段的性质证明即可.
解答 证明:(1)∵四边形ABCD是平行四边形ABCD,
∴AD∥BC,AD=BC,
又∵CE∥AF,
∴四边形AECF是平行四边形,
∴AE=FC,
∴DF=BE,
又∵DF∥BE,
∴四边形DEBF是平行四边形,
∴DE∥BF;
(2)延长AF,DE交BC的延长线于点N,M,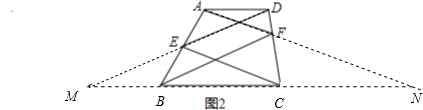
∵AD∥BM,
∴$\frac{AD}{BM}=\frac{AE}{BE}$,
∵EC∥AN,
∴$\frac{AE}{EB}=\frac{CN}{BC}$,
∵AD∥CN,
∴$\frac{AD}{CN}=\frac{DF}{FC}$,
∴$\frac{AD}{BM}=\frac{CN}{BC}$,
∴$\frac{AD}{CN}=\frac{MB}{BC}$,
∴$\frac{DF}{FC}=\frac{MB}{BC}$,
∴BF∥DM,
∴DE∥BF.
点评 此题主要考查了平行四边形的判定与性质,得出四边形AECF是平行四边形是解题关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
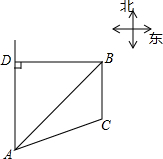 已知B港口位于A观测点的东北方向,且其到A观测点正北方向的距离BD的长为16千米,一艘货轮从B港口以48千米/时的速度沿如图所示的BC方向航行,15分后到达C处,现测得C处位于A观测点北偏东75°方向,求此时货轮与A观测点之间的距离AC的长(精确大0.1千米)
已知B港口位于A观测点的东北方向,且其到A观测点正北方向的距离BD的长为16千米,一艘货轮从B港口以48千米/时的速度沿如图所示的BC方向航行,15分后到达C处,现测得C处位于A观测点北偏东75°方向,求此时货轮与A观测点之间的距离AC的长(精确大0.1千米)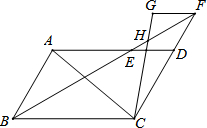 ?ABCD中,∠ABC=60°,∠ABC的角平分线与AD交于点E,交CD延长线于点F,FG∥DA且FG=DE,连接CG,CG与EF交于点H.
?ABCD中,∠ABC=60°,∠ABC的角平分线与AD交于点E,交CD延长线于点F,FG∥DA且FG=DE,连接CG,CG与EF交于点H.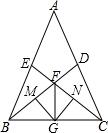 如图,在△ABC中,点E在AB上,点D在AC上,G为BC的中点,BE=CD,∠BEC=∠CDB,BD与CE相交于点F,GM⊥BF,GN⊥CF,垂足分别为M,N.
如图,在△ABC中,点E在AB上,点D在AC上,G为BC的中点,BE=CD,∠BEC=∠CDB,BD与CE相交于点F,GM⊥BF,GN⊥CF,垂足分别为M,N. 如图,在平面直角坐标系中,△AOB是等边三角形,且边长为2,则点A的坐标为A(1,$\sqrt{3}$).
如图,在平面直角坐标系中,△AOB是等边三角形,且边长为2,则点A的坐标为A(1,$\sqrt{3}$).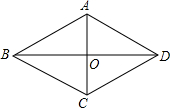 如图,四边形ABCD是菱形,对角线AC、BD相交于O,如果菱形的周长是40cm,它的一条对角线AC长10cm,
如图,四边形ABCD是菱形,对角线AC、BD相交于O,如果菱形的周长是40cm,它的一条对角线AC长10cm,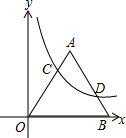 在平面直角坐标系中,等边三角形OAB中OB在x轴上,点A在第一象限,双曲线y=$\frac{4\sqrt{3}}{x}$交OA于点C,交AB于点D,若OC:BD=2:1,则OB=5.
在平面直角坐标系中,等边三角形OAB中OB在x轴上,点A在第一象限,双曲线y=$\frac{4\sqrt{3}}{x}$交OA于点C,交AB于点D,若OC:BD=2:1,则OB=5. 如图,直角坐标系xOy中,正方形OABC的边AB与反比例函数y=$\frac{1}{x}$(x>0)的图象交于点D,且AD:DB=1:8,则:
如图,直角坐标系xOy中,正方形OABC的边AB与反比例函数y=$\frac{1}{x}$(x>0)的图象交于点D,且AD:DB=1:8,则: