题目内容
13.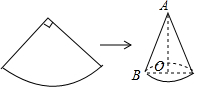 如图,现有一圆心角为90°,半径为80cm的扇形铁片,用它恰好围成一个圆锥形的量筒(接缝忽略不计),用其它铁片再做一个圆形盖子把量筒底面密封.
如图,现有一圆心角为90°,半径为80cm的扇形铁片,用它恰好围成一个圆锥形的量筒(接缝忽略不计),用其它铁片再做一个圆形盖子把量筒底面密封.(1)这个圆锥底面的圆形盖子的半径为多少?
(2)求这个圆锥的高.
分析 (1)根据扇形的弧长等于圆锥的底面周长,利用扇形的弧长公式即可求得圆锥的底面周长,然后根据圆的周长公式即可求解;
(2)利用勾股定理求得圆锥的高即可.
解答 解:(1)圆锥的底面周长是:$\frac{90π×80}{180}$=40πcm.
设圆锥底面圆的半径是r,则
2πr=40π.
解得:r=20cm;
(2)圆锥的高为:$\sqrt{8{0}^{2}-2{0}^{2}}$=20$\sqrt{3}$cm.
点评 本题考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.

练习册系列答案
相关题目
 如图,E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为点C和点D.
如图,E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为点C和点D.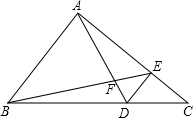 已知△ABC,其中DE与AB平行,已知△DEC的面积为5,且S△ABF:S△AEF=4:1,求△ABC的面积是80.
已知△ABC,其中DE与AB平行,已知△DEC的面积为5,且S△ABF:S△AEF=4:1,求△ABC的面积是80.