题目内容
20.已知关于x的一元二次方程(m-1)x2+(2m-1)x2+m-$\frac{3}{4}$=0(1)若方程有两个相等的实数根时,求m的值.
(2)当方程有两个实数根时,求出m的最小正整数的值.
分析 计算出根的判别式,则
(1)若方程有两个相等的实数根时,△=0求m的值.
(2)当方程有两个实数根时,△≥0且m-1≠0求得m的取值范围,得出答案即可.
解答 解:△=(2m-1)2-4(m-1)(m-$\frac{3}{4}$)=3m-2;
(1)∵方程有两个相等的实数根,
∴3m-2=0,
∴m=$\frac{2}{3}$;
(2)∵方程有两个实数根,
∴3m-2≥0,且m-1≠0,
∴m≥$\frac{2}{3}$且m≠1,
∵m是最小正整数,
∴m=2.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.以及一元二次方程的意义.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
8.过年了,全班同学每人互发一条短信,共发了45条,设全班有x名同学,列方程为( )
| A. | $\frac{1}{2}x(x-1)=45$ | B. | x(x-1)=45 | C. | x(x+1)=45 | D. | 2x(x-1)=45 |
9.为了促进义务教育办学条件均衡,2015年某市投入4800000元资金为部分学校添置实验仪器及体、音、美器材.4800000这个数用科学记数法表示为( )
| A. | 48×105 | B. | 4.8×106 | C. | 0.48×107 | D. | 4.8×107 |
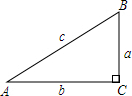 已知,在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c.
已知,在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c. 如图,△ABC内接于⊙O,AD是△ABC的边BC上的高,AE是⊙O的直径,连接BE,求证:AB•AC=AD•AE.
如图,△ABC内接于⊙O,AD是△ABC的边BC上的高,AE是⊙O的直径,连接BE,求证:AB•AC=AD•AE.