题目内容
11.在Rt△ABC中,∠C=Rt∠,根据下列条件解直角三角形(长度精确到0.1.角度精确到1″)(1)c=7,∠A=36°;
(2)a=6,cosB=$\frac{\sqrt{5}-1}{2}$.
分析 (1)根据直角三角形中边角之间的关系,由c=7,∠A=36°,可以得到∠B的度数,从而可以求得其它的量,进而可以解答本题;
(2)根据直角三角形中边角之间的关系,由a=6,cosB=$\frac{\sqrt{5}-1}{2}$,可以得到c的值,从而可以取得其它的量,进而可以解答本题.
解答 解:(1)∵在Rt△ABC中,∠C=90°,c=7,∠A=36°,sinA=$\frac{a}{c}$,cosA=$\frac{b}{c}$,
∴∠B=90°-36°=54°,a=7×sin36°,b=7×cos36°.
∴a≈4.1,b≈5.7.
即∠B=54°,a≈4.1,b≈5.7.
(2))∵在Rt△ABC中,∠C=90°,a=6,cosB=$\frac{\sqrt{5}-1}{2}$,cosB=$\frac{a}{c}$,
∴c=$\frac{a}{cosB}=\frac{6}{\frac{\sqrt{5}-1}{2}}=\frac{12}{\sqrt{5}-1}=3\sqrt{5}+3$≈9.7.
∴b=$\sqrt{{c}^{2}-{a}^{2}}=\sqrt{(3\sqrt{5}+3)^{2}-{6}^{2}}$=$\sqrt{18+18\sqrt{5}}$≈7.6.
∵cosB=$\frac{\sqrt{5}-1}{2}$,
∴∠B≈55.389°=55°+0.389×60′=55°+23′+0.34×60″=55°23′+20.4″≈55°23′20″.
∴∠A=90°-55°23′20″=34°36′40″.
即b≈7.6,c≈9.7,∠A=34°36′40″,∠B=55°23′20″.
点评 本题考查解直角三角形,解题的关键是明确直角三角形中边角的关系.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
1.若( )•3ab2=6a2b3,则括号内应填的代数式是( )
| A. | 2a | B. | ab | C. | 2ab | D. | 3ab |
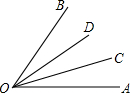 如图所示,如果OC,OD是∠AOB的三等分线,那么∠AOC=∠BOD=∠DOC,∠BOD=$\frac{1}{3}$∠AOB,∠AOD=22∠BOD或2∠DOC或2∠COA.
如图所示,如果OC,OD是∠AOB的三等分线,那么∠AOC=∠BOD=∠DOC,∠BOD=$\frac{1}{3}$∠AOB,∠AOD=22∠BOD或2∠DOC或2∠COA.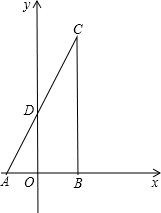 已知△ABC中,∠B=90°,∠A=60°,AB=6,把它放在平面坐标系中,使A,B两点关于y轴对称,边AC交y轴于点D,如图所示,点P是AC边上的动点,点E是x轴上的动点,且PB=PE,设PA=t,
已知△ABC中,∠B=90°,∠A=60°,AB=6,把它放在平面坐标系中,使A,B两点关于y轴对称,边AC交y轴于点D,如图所示,点P是AC边上的动点,点E是x轴上的动点,且PB=PE,设PA=t,