Question

5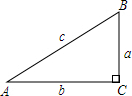．已知，在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c．
（1）利用三角函数的定义及勾股定理，求证：sin²A+cos²A=1；
（2）请你探究sinA，cosA与tanA之间的关系；
（3）已知$\frac{sinα+cosα}{2sinα+cosα}$=$\frac{2}{3}$，利用第（2）的结论可得tanα的值为1．

Answer 1

分析 （1）根据锐角三角函数的定义可以表示出sinA、cosA，根据勾股定理得到三边的关系，从而可以证明结论成立；
（2）根据锐角三角函数的定义可以分别表示出sinA、cosA、tanA，从而可以得到它们之间的关系；
（3）根据（2）中的结论可以得到tanα的值．

解答 （1）证明：∵在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，
∴sinA=$\frac{a}{c}$，cosA=$\frac{b}{c}$，a²+b²=c²．
∴$si{n}^{2}A+co{s}^{2}A=\frac{{a}^{2}}{{c}^{2}}+\frac{{b}^{2}}{{c}^{2}}=\frac{{a}^{2}+{b}^{2}}{{c}^{2}}$=$\frac{{c}^{2}}{{c}^{2}}=1$．
即sin²A+cos²A=1．
（2）解：∵在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，
∴sinA=$\frac{a}{c}$，cosA=$\frac{b}{c}$，tanA=$\frac{a}{b}$．
∴$\frac{sinA}{cosA}=\frac{\frac{a}{c}}{\frac{b}{c}}=\frac{a}{b}=tanA$．
即sinA，cosA与tanA之间的关系是：tanA=$\frac{sinA}{cosA}$．
（3）解：∵$\frac{sinα+cosα}{2sinα+cosα}$=$\frac{2}{3}$，
∴$\frac{\frac{sinα}{cosα}+\frac{cosα}{cosα}}{2×\frac{sinα}{cosα}+\frac{cosα}{cosα}}=\frac{tanα+1}{2tanα+1}=\frac{2}{3}$．
解得，tanα=1．
故答案为：1．

点评 本题考查解直角三角形，解题的关键是明确锐角三角函数，找出所求问题需要的条件．