题目内容
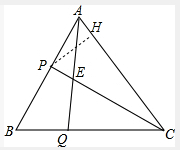
 等边三角形ABC的边长为3,点P、Q分别是AB、BC上的动点(点P、Q与三角形ABC的顶点不重合),且AP=BQ,AQ、CP相交于E.
等边三角形ABC的边长为3,点P、Q分别是AB、BC上的动点(点P、Q与三角形ABC的顶点不重合),且AP=BQ,AQ、CP相交于E.(1)求证:△ABQ≌△CAP;
(2)求证:△APE∽△ABQ;
(3)设线段AP为x,线段CP为y,求y关于x的函数解析式,并写出定义域.
考点:相似三角形的判定与性质,全等三角形的判定与性质,等边三角形的性质
专题:常规题型
分析:(1)根据题干中给出条件即可证明△ABQ≌△CAP;
(2)过P作PH⊥AC交AC于H,构建RT△PCH即可解题.
(2)过P作PH⊥AC交AC于H,构建RT△PCH即可解题.
解答:解:(1)在△ABQ和△CAP中,
,
∴△ABQ≌△CAP(SAS),
(2)∵△ABQ≌△CAP,
∴∠APE=∠AQB,
∵∠BAQ=∠PAE
∴△APE∽△ABQ;
(3)过P作PH⊥AC交AC于H,
由∠BAC=60°,AP=x,
∴AH=
,PH=
.
CH=3-
,
∴y2=PC2=PH2+CH2,
∴y2=(
)2+(3-
)2=
x2+9-3x+
x2
∴y=
.0<x<3.
|
∴△ABQ≌△CAP(SAS),
(2)∵△ABQ≌△CAP,
∴∠APE=∠AQB,
∵∠BAQ=∠PAE
∴△APE∽△ABQ;
(3)过P作PH⊥AC交AC于H,

由∠BAC=60°,AP=x,
∴AH=
| x |
| 2 |
| ||
| 2 |
CH=3-
| x |
| 2 |
∴y2=PC2=PH2+CH2,
∴y2=(
| ||
| 2 |
| x |
| 2 |
| 3 |
| 4 |
| 1 |
| 4 |
∴y=
| x2-3x+9 |
点评:本题考查了全等三角形的判定,考查了相似三角形的判定,考查了全等三角形对应角相等的性质.

练习册系列答案
相关题目
 在一块钝角三角形的余料上,加工成正方形零件,使正方形的至少3个顶点都在三角形边上,若三角形的三边长分别为a、b、c,且a>b>c,问正方形的2个顶点放在哪条边上可使加工出来的正方形零件面积最大?
在一块钝角三角形的余料上,加工成正方形零件,使正方形的至少3个顶点都在三角形边上,若三角形的三边长分别为a、b、c,且a>b>c,问正方形的2个顶点放在哪条边上可使加工出来的正方形零件面积最大? 如图,抛物线y=-
如图,抛物线y=-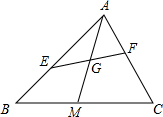 如图,在△ABC中,AM是中线,AB=8,AC=6,E、F分别在AB、AC上,且AE=2AF,EF交AM于点G,则
如图,在△ABC中,AM是中线,AB=8,AC=6,E、F分别在AB、AC上,且AE=2AF,EF交AM于点G,则 如图,AB=m,CD=n,AD⊥BD,BC相交于E,求证:cos∠BED=
如图,AB=m,CD=n,AD⊥BD,BC相交于E,求证:cos∠BED= 如图,△ABC中,DE∥BC,
如图,△ABC中,DE∥BC,