题目内容
如果一条抛物线y=ax2+bx+c的顶点在x轴上(不在原点),那么以该抛物线的顶点和与y轴的交点及原点所构成的三角形称为此抛物线的“坐标轴三角形”
(1)此坐标轴三角形是一个什么三角形?
(2)若抛物线y=x2+bx+c(b<0)的“坐标轴三角形”是等腰三角形,求解析式;
(3)△OAB是抛物线y=x2+mx+n的“坐标轴三角形”,是否存在以y轴为对称轴的等边三角形?若存在,需将y=x2+mx+n进行怎样的平移才能恰好经过A、C两点,并求平移后的解析式.
(1)此坐标轴三角形是一个什么三角形?
(2)若抛物线y=x2+bx+c(b<0)的“坐标轴三角形”是等腰三角形,求解析式;
(3)△OAB是抛物线y=x2+mx+n的“坐标轴三角形”,是否存在以y轴为对称轴的等边三角形?若存在,需将y=x2+mx+n进行怎样的平移才能恰好经过A、C两点,并求平移后的解析式.
考点:二次函数综合题
专题:压轴题
分析:(1)求出以点O为顶点的角是直角,然后判断即可;
(2)根据抛物线顶点在x轴上列式表示出b、c的关系,再求出抛物线与坐标轴的交点,然后根据等腰三角形两腰相等列出方程求解即可;
(3)根据抛物线顶点在x轴上列式表示出m、n的关系,表示出抛物线与坐标轴的交点,然后利用等边三角形的性质列出方程求出m、n,再根据等边三角形的对称性解答.
(2)根据抛物线顶点在x轴上列式表示出b、c的关系,再求出抛物线与坐标轴的交点,然后根据等腰三角形两腰相等列出方程求解即可;
(3)根据抛物线顶点在x轴上列式表示出m、n的关系,表示出抛物线与坐标轴的交点,然后利用等边三角形的性质列出方程求出m、n,再根据等边三角形的对称性解答.
解答:解:(1)∵顶点在x轴上,另一交点在y轴上,
∴以点O为顶点的角是直角,
∴坐标轴三角形是直角三角形;
(2)∵抛物线顶点在x轴上,
∴
=0,
∴b2=4c,
令x=0,则y=c,
抛物线与x轴的交点坐标为(-
,0),
∵“坐标轴三角形”是等腰三角形,
∴-
=c,
∴b=-2c,
∴(-2c)2=4c,
解得c1=1,c2=0(舍去),
∴b=-2,
∴抛物线解析式为y=x2-2x+1;
(3)∵抛物线顶点在x轴上,
∴
=0,
∴m2=4n,
令x=0,则y=n,
抛物线与x轴的交点坐标为(-
,0),
∵“坐标轴三角形”是等边三角形,
∴n=
•|-
|
∴|m|=
n,
∴(
n)2=4n,
解得n1=3,c2=0(舍去),
∴m=±2
,
∴抛物线解析式为y=x2+2
x+3或y=x2-2
x+3,
∵等边三角形以y轴为对称轴,
∴y=x2+2
x+3平移后的解析式为y=x2-2
x+3,
y=x2-2
x+3平移后的解析式为y=x2+2
x+3.
∴以点O为顶点的角是直角,
∴坐标轴三角形是直角三角形;
(2)∵抛物线顶点在x轴上,
∴
| 4×1×c-b2 |
| 4×1 |
∴b2=4c,
令x=0,则y=c,
抛物线与x轴的交点坐标为(-
| b |
| 2 |
∵“坐标轴三角形”是等腰三角形,
∴-
| b |
| 2 |
∴b=-2c,
∴(-2c)2=4c,
解得c1=1,c2=0(舍去),
∴b=-2,
∴抛物线解析式为y=x2-2x+1;
(3)∵抛物线顶点在x轴上,
∴
| 4×1×n-m2 |
| 4×1 |
∴m2=4n,
令x=0,则y=n,
抛物线与x轴的交点坐标为(-
| m |
| 2 |
∵“坐标轴三角形”是等边三角形,
∴n=
| 3 |
| m |
| 2 |
∴|m|=
2
| ||
| 3 |
∴(
2
| ||
| 3 |
解得n1=3,c2=0(舍去),
∴m=±2
| 3 |
∴抛物线解析式为y=x2+2
| 3 |
| 3 |
∵等边三角形以y轴为对称轴,
∴y=x2+2
| 3 |
| 3 |
y=x2-2
| 3 |
| 3 |
点评:本题是二次函数综合题融入了新定义的形式,涉及到:二次函数的性质及解析式的确定、等腰直角三角形的判定和性质、等边三角形的性质,难度不大,重在考查基础知识的掌握情况.

练习册系列答案
相关题目
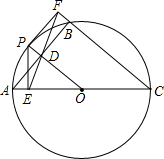 已知,⊙O是△ABC的外接圆,AC是直径,过O点作OD⊥AB于点D,延长DO交⊙O于点P,作PE⊥AC与点E,射线DE交BC的延长线于点F,求证:PF是⊙O的切线.
已知,⊙O是△ABC的外接圆,AC是直径,过O点作OD⊥AB于点D,延长DO交⊙O于点P,作PE⊥AC与点E,射线DE交BC的延长线于点F,求证:PF是⊙O的切线.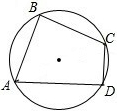 如图,在圆内接四边形ABCD中,∠A=60°,∠B=90°,AB=2,CD=1,则BC=
如图,在圆内接四边形ABCD中,∠A=60°,∠B=90°,AB=2,CD=1,则BC=