题目内容
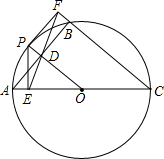 已知,⊙O是△ABC的外接圆,AC是直径,过O点作OD⊥AB于点D,延长DO交⊙O于点P,作PE⊥AC与点E,射线DE交BC的延长线于点F,求证:PF是⊙O的切线.
已知,⊙O是△ABC的外接圆,AC是直径,过O点作OD⊥AB于点D,延长DO交⊙O于点P,作PE⊥AC与点E,射线DE交BC的延长线于点F,求证:PF是⊙O的切线.考点:切线的判定
专题:证明题
分析:利用圆周角定理由AC是直径得∠ABC=90°,由OD⊥AB,根据垂径定理得AD=BD,易得OD∥BC,BC=2OD,再根据“AAS”证明△OPE≌△OAD,得到OD=OE,
则PD=AE,由于OD∥CF,可判断△CEF为等腰三角形,则CE=CF,然后利用线段之间的代换得到PD=BF,于是可判断四边形PDBF为平行四边形,得到PF∥DB,所以OP⊥PF,然后根据切线的判定定理可得PF为⊙O的切线.
则PD=AE,由于OD∥CF,可判断△CEF为等腰三角形,则CE=CF,然后利用线段之间的代换得到PD=BF,于是可判断四边形PDBF为平行四边形,得到PF∥DB,所以OP⊥PF,然后根据切线的判定定理可得PF为⊙O的切线.
解答: 证明:∵AC是直径,
证明:∵AC是直径,
∴∠ABC=90°,
∵OD⊥AB,
∴∠ADO=90°,AD=BD,
∴OD∥BC,BC=2OD,
∵PE⊥OA,
∴∠PEO=90°,
在△OPE和△OAD中,
,
∴△OPE≌△OAD(AAS),
∴OD=OE,
∴PD=AE,
∵OD∥CF,
∴CE=CF,
∴AC-AE=BC+BF,
AC-AE=2OD+BF
AC-AE=2(OP-PD)+BF,
∴AC-PD=2OP-2PD+BF,
∴PD=BF,
∴四边形PDBF为平行四边形,
∴PF∥DB,
∴OP⊥PF,
∴PF为⊙O的切线.
 证明:∵AC是直径,
证明:∵AC是直径,∴∠ABC=90°,
∵OD⊥AB,
∴∠ADO=90°,AD=BD,
∴OD∥BC,BC=2OD,
∵PE⊥OA,
∴∠PEO=90°,
在△OPE和△OAD中,
|
∴△OPE≌△OAD(AAS),
∴OD=OE,
∴PD=AE,
∵OD∥CF,
∴CE=CF,
∴AC-AE=BC+BF,
AC-AE=2OD+BF
AC-AE=2(OP-PD)+BF,
∴AC-PD=2OP-2PD+BF,
∴PD=BF,
∴四边形PDBF为平行四边形,
∴PF∥DB,
∴OP⊥PF,
∴PF为⊙O的切线.
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了三角形全等的判定与性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
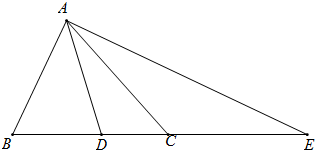 的度数.
的度数. 如图,在△ABC中,AB=13,AC=15,BC边上的高AD=12.
如图,在△ABC中,AB=13,AC=15,BC边上的高AD=12.