题目内容
已知关于x的一次函数y=3x+a和y=-4x-b交于点A（a-2，a+b-2），且x＜a+b（其中a，b，为实数），求y的取值范围．
考点：两条直线相交或平行问题
专题：
分析：先解由一次函数组成的方程组求出x，y，再求出a，b的值，由增减函数求出y的取值范围．
解答：解：解由一次函数组成的方程组
，得
，
∵一次函数y=3x+a和y=-4x-b交于点A（a-2，a+b-2），
∴a-b=
，a+b-2=
，解得
，
∵x＜a+b，
∴x＜
+
=2，
∵y=3x+
是增函数，y=-4x-
是减函数，
∴-
＜y＜
．
|
|
∵一次函数y=3x+a和y=-4x-b交于点A（a-2，a+b-2），
∴a-b=
| -a-b |
| 7 |
| 4a-3b |
| 7 |
|
∵x＜a+b，
∴x＜
| 6 |
| 7 |
| 8 |
| 7 |
∵y=3x+
| 6 |
| 7 |
| 8 |
| 7 |
∴-
| 64 |
| 7 |
| 48 |
| 7 |
点评：本题主要考查了两条直线相交或平行问题，解题的关键是求出a，b的值．
练习册系列答案
相关题目
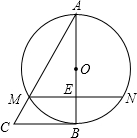如图，在△ABC中，以AB为直径的⊙O交AC于点M，弦MN∥BC交AB于点E，且ME=1，AM=2，AE=
如图，在△ABC中，∠ABC、∠ACB的平分线交于点O．