题目内容
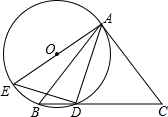
16. 如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,过点C作CE⊥DB交DB的延长线于点E,直线AB与CE相交于点F.
如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,过点C作CE⊥DB交DB的延长线于点E,直线AB与CE相交于点F.(1)求证:CF为⊙O的切线;
(2)填空:当∠CAB的度数为30°时,四边形ACFD是菱形.
分析 (1)连结OC,如图,由于∠A=∠OCA,则根据三角形外角性质得∠BOC=2∠A,而∠ABD=2∠BAC,所以∠ABD=∠BOC,根据平行线的判定得到OC∥BD,再CE⊥BD得到OC⊥CE,然后根据切线的判定定理得CF为⊙O的切线;
(2)根据三角形的内角和得到∠F=30°,根据等腰三角形的性质得到AC=CF,连接AD,根据平行线的性质得到∠DAF=∠F=30°,根据全等三角形的性质得到AD=AC,由菱形的判定定理即可得到结论.
解答 (1)证明:连结OC,如图,
∵OA=OC,
∴∠A=∠OCA,
∴∠BOC=∠A+∠OCA=2∠A,
∵∠ABD=2∠BAC,
∴∠ABD=∠BOC,
∴OC∥BD,
∵CE⊥BD,
∴OC⊥CE,
∴CF为⊙O的切线;
(2)当∠CAB的度数为30°时,四边形ACFD是菱形,
理由:∵∠A=30°,
∴∠COF=60°,
∴∠F=30°,
∴∠A=∠F,
∴AC=CF,
连接AD,
∵AB是⊙O的直径,
∴AD⊥BD,
∴AD∥CF,
∴∠DAF=∠F=30°,
在△ACB与△ADB中,$\left\{\begin{array}{l}{∠CAB=∠DAB=30°}\\{∠ACB=∠D=90°}\\{AB=AB}\end{array}\right.$,
∴△ACB≌△ADB,
∴AD=AC,
∴AD=CF,
∵AD∥CF,
∴四边形ACFD是菱形.
故答案为:30°.
点评 本题考查了切线的判定,全等三角形的判定和性质,菱形的判定,圆周角定理,等腰三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
4.下列计算结果等于a5的是( )
| A. | a3+a2 | B. | a3•a2 | C. | (a3)2 | D. | a10÷a2 |
11.下面四个图形中,是三棱柱的平面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
8.某企业不断引进科技提高生产率,在工人数量和每个人的生产效益方面均获得提升,2014年工人总数250人,生产总值为100亿元,2016年工人总数上升到400人,生产总值达到736亿元,设2015年和2016年每位工人的生产效益平均增长百分率为x,则下列方程正确的是( )
| A. | $\frac{100}{250}$(1+x)2=$\frac{736}{400}$ | B. | 100(1+x)2=736 | ||
| C. | 250(1+x)2=100 | D. | $\frac{736}{400}$(1-x)2=$\frac{100}{250}$ |
5.因式分解x2y-4y的结果是( )
| A. | y(x2-4) | B. | y(x-2)2 | C. | y(x+4)(x-4) | D. | y(x+2)(x-2) |
6.下列运算正确的是( )
| A. | a6÷a2=a3 | B. | a3•a2=a6 | C. | (3a3)2=6a6 | D. | a3-a3=0 |
 如图,在△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A、B、D三点作⊙O,AE是⊙O的直径,连接DE.
如图,在△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A、B、D三点作⊙O,AE是⊙O的直径,连接DE. 如图,已知AB为⊙O直径,过⊙O上一点C作⊙O的切线,交AB延长线于点E,作AD⊥CE,交EC延长线于D,交⊙O于点F,设∠ABC=α(0°<α<90°).
如图,已知AB为⊙O直径,过⊙O上一点C作⊙O的切线,交AB延长线于点E,作AD⊥CE,交EC延长线于D,交⊙O于点F,设∠ABC=α(0°<α<90°).