题目内容
20.阅读下面一题的解答过程,请判断是否正确.若不正确,请写出正确的解答.已知x,y是实数,化简x$\sqrt{-\frac{y}{{x}^{2}}}$+y$\sqrt{-\frac{x}{{y}^{2}}}$.
解:原式=$\sqrt{{x}^{2}•(-\frac{y}{{x}^{2}})}$+$\sqrt{{y}^{2}•(-\frac{x}{{y}^{2}})}$=$\sqrt{-y}$+$\sqrt{-x}$.
分析 根据二次根式的定义可得出x,y都是负数,进而化简得出答案.
解答 解:解答过程错误,
正确结果如下:原式=-$\sqrt{{x}^{2}•(-\frac{y}{{x}^{2}})}$-$\sqrt{{y}^{2}•(-\frac{x}{{y}^{2}})}$=-$\sqrt{-y}$-$\sqrt{-x}$.
点评 此题主要考查了二次根式的化简求值,正确得出x,y的符号是解题关键.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
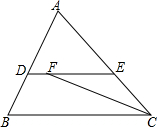 如图,在△ABC中,∠A=∠B,点D、E分别在AB、AC上,DE∥BC,△ACB的平分线交DE于点F,BC=5,AE=3.求DF的长.
如图,在△ABC中,∠A=∠B,点D、E分别在AB、AC上,DE∥BC,△ACB的平分线交DE于点F,BC=5,AE=3.求DF的长.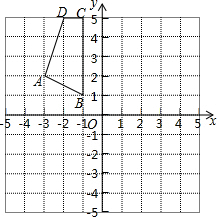 四边形ABCD在平面直角坐标系中的位置如图所示.
四边形ABCD在平面直角坐标系中的位置如图所示.