Question

14．在矩形ABCD中，已知：AB=a，BC=b，动点E从点A出发沿着边AD向点D运动．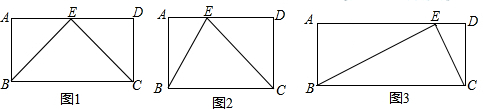

（1）如图1所示，当a=2，b=4，点E运动到边AD的中点时，求证：BE⊥CE；
（2）如图2所示，当a=2，b=3时，点E在运动过程中，是否存在BEC=90°？若存在，请给出证明；若不存在，请说明理由；
（3）如图3所示，当a=2，b=5时，点E在运动的过程中，若以A，B，E为顶点的三角形与以D，C，E为顶点的三角形相似，求此时AE的长度．

Answer 1

分析 （1）当点E运动到边AD的中点时，AE=AB，DE=DC，故此△AEB和△DEC为等腰直角三角形，从而可证明∠BEC=90°；
（2）以BC为直径作圆0，过点O作OF⊥AD垂足为F，可知r=1.5，OF=2，d＞r，故此直线AD与圆0相离，所以∠BEC＜90°；
（3）根据题意画出图形，然后根据相似三角形的性质列出比例式，从而可求得AE的长．

解答 解：（1）∵E是AD的中点，
∴AE=DE=2．
∵AB=DC=2．
∴AE=AB，DE=DC．
∵ABCD为矩形，
∴∠A=∠D=90°．
∴△AEB和△DEC均为等腰直角三角形．
∴∠AEB=45°，∠DEC=45°．
∴∠BEC=180°-45°-45°=90°．
∴BE⊥EC．
（2）不存在．
理由：以BC为直径作圆0，过点O作OF⊥AD垂足为F．

∵BC=3，
∴圆O的半径r=1.5，
∵∠ABO=∠A=∠OFA=90°，
∴四边形ABOF为矩形．
∴OF=AB=2．
∴d＞r，
∴直线AD与圆0相离．
∴点E在圆O外．
∴∠BEC＜90°；
（3）如图3所示．

①设AE=x，则ED=5-x．
∵△EAB∽△CDE，
∴$\frac{DC}{ED}=\frac{AE}{AD}$，即$\frac{2}{5-x}=\frac{x}{2}$．
解得：x₁=4，x₂=1（舍去），
∴AE=4．
②当点E位于E′处时．
∵△AE′B∽△DE′C．
∴$\frac{AE′}{DE′}=\frac{AB}{DC}=1$．
∴AE′=DE′．
∴AE′=2.5，即AE=2.5．
③当点E位于E″处时．
∵△ABE″∽△DE″C，
∴$\frac{AE″}{AB}=\frac{DC}{DE″}$，即$\frac{x}{2}=\frac{2}{5-x}$．
解得：x₁=1，x₂=4（舍去）．
综上所述，若以A，B，E为顶点的三角形与以D，C，E为顶点的三角形相似，AE=1或AE=2.5，或AE=4．

点评 本题主要考查的是矩形的性质、相似三角形的性质和判定、等腰直角三角形的性质和判定的综合应用，根据相似三角形的性质，结合点E的位置，列出关于AE长度的比例式是解题的关键．