题目内容
4.已知某等腰三角形的三边长都是方程x2-3x+2=0的解,则此三角形的周长是( )| A. | 3或5 | B. | 5或6 | C. | 3或6 | D. | 3或5或6 |
分析 利用因式分解法求出方程的解,分类讨论即可确定出此三角形周长.
解答 解:方程x2-3x+2=0,分解得:(x-1)(x-2)=0,
解得:x=1或x=2,
若1为腰,三角形三边为1,1,2,不能构成三角形,舍去;
若1为底,三角形三角形为1,2,2,周长为1+2+2=5,
若三角形为等边三角形,周长为1+1+1=3或2+2+2=6,
综上,此三角形周长为3或5或6,
故选D.
点评 此题考查了解一元二次方程-因式分解法,三角形三边关系,以及等腰三角形的性质,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
12.已知点(-1,y1),(2,y2)都在直线y=-$\frac{1}{2}$x+1上,则y1,y2大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能比较 |
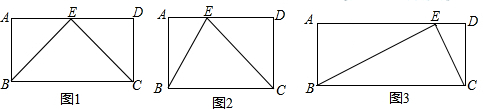
 如图,在面积为21cm2的矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD交AD于点F,若EF=3,则AE=5cm.
如图,在面积为21cm2的矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD交AD于点F,若EF=3,则AE=5cm.
 如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去.则第2016个正方形的边长为($\sqrt{2}$)2015.
如图,设四边形ABCD是边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去.则第2016个正方形的边长为($\sqrt{2}$)2015.