题目内容
17. 如图所示,直线l是四边形ABCD的对称轴,若AB=CD,有下面4个结论:
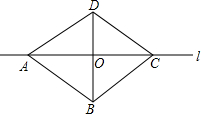
如图所示,直线l是四边形ABCD的对称轴,若AB=CD,有下面4个结论:①AB∥CD;②AC⊥BD;③AO=CO;④AB⊥BC.
其中正确的结论有几个( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 根据轴对称的性质得到直线l垂直平分BD,则根据线段垂直平分线的性质得AB=AD,CD=CB,由于AB=CD,则AB=BC=CD=BC,于是可判断四边形ABCD为菱形,然后根据菱形的性质对4个结论进行判断.
解答 解:∵直线l是四边形ABCD的对称轴,
∴直线l垂直平分BD,
∴AB=AD,CD=CB,
∵AB=CD,
∴AB=BC=CD=BC,
∴四边形ABCD为菱形,
∴AC⊥BD,AB∥CD,OA=OC,所以①②③正确.
故选:B.
点评 本题考查了轴对称的性质:如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.也考查了菱形的判定与性质.

练习册系列答案
相关题目
7.下列方程是一元二次方程的是( )
| A. | ax2-2x+=0(a是已知数) | B. | 3x2+2x-4=3x2 | ||
| C. | 5x2-2x=0 | D. | $\frac{{x}^{3}+2x}{x}$=1 |
 如图,反比例函数y=$\frac{18}{x}$的图象过矩形OABC的顶点B,OA、OC分别在x轴、y轴的正半轴上,OA;OC=1:2,矩形OABC的对角线交于点E.
如图,反比例函数y=$\frac{18}{x}$的图象过矩形OABC的顶点B,OA、OC分别在x轴、y轴的正半轴上,OA;OC=1:2,矩形OABC的对角线交于点E. 如图,在各个手指间标记字母A,B,C,D.请按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,4,….当字母C第2015次出现时,数到的数恰好是6045.
如图,在各个手指间标记字母A,B,C,D.请按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,4,….当字母C第2015次出现时,数到的数恰好是6045.