题目内容
9. 如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )
如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )| A. | 32 | B. | 24 | C. | 16 | D. | 8 |
分析 先根据等边三角形的各边相等且各角为60°得:∠B1A1A2=60°,A1B1=A1A2,再利用外角定理求∠OB1A1=30°,则∠MON=∠OB1A1,由等角对等边得:B1A1=OA1=2,得出△A1B1A2的边长为2,再依次同理得出:△A2B2A3的边长为4,△A4B4A5的边长为:24=16,则△A5B5A6的边长为:25=32.
解答 解:∵△A1B1A2为等边三角形,
∴∠B1A1A2=60°,A1B1=A1A2,
∵∠MON=30°,
∴∠OB1A1=60°-30°=30°,
∴∠MON=∠OB1A1,
∴B1A1=OA1=2,
∴△A1B1A2的边长为2,
同理得:∠OB2A2=30°,
∴OA2=A2B2=OA1+A1A2=2+2=4,
∴△A2B2A3的边长为4,
同理可得:、△A3B3A4的边长为:23=8,
△A4B4A5的边长为:24=16,
则△A5B5A6的边长为:25=32,
故选A.
点评 本题考查了等边三角形的性质和外角定理,难度不大,需要运用类比的思想,依次求出各等边三角形的边长,并总结规律,才能得出结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.化简$\frac{-36}{-12}$的结果是( )
| A. | 3 | B. | -3 | C. | -4 | D. | 24 |
20.如图,将四根长度相等的细木条首尾相接钉成四边形ABCD,当∠B=90°时,测得AC=4,改变它的形状使∠B=60°,此时AC的长度为( )
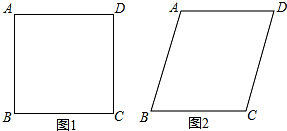

| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{6}$ | D. | 2$\sqrt{2}$ |
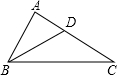 如图,在△ABC中,∠A=90°,BD平分∠ABC,∠C=30°,AD=2,AB=2$\sqrt{3}$,那么S△ABC=6$\sqrt{3}$.
如图,在△ABC中,∠A=90°,BD平分∠ABC,∠C=30°,AD=2,AB=2$\sqrt{3}$,那么S△ABC=6$\sqrt{3}$. 如图,⊙O是△ABC的外接圆,∠BOC=136°,则∠A的大小是68°.
如图,⊙O是△ABC的外接圆,∠BOC=136°,则∠A的大小是68°.