题目内容
8.在△ABC中,AC=$\sqrt{14}$,BC=5$\sqrt{2}$,AB=6,则△ABC是直角三角形.分析 欲求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可.
解答 解:在△ABC中,AC=$\sqrt{14}$,BC=5$\sqrt{2}$,AB=6,
∵62+($\sqrt{14}$)2=(5$\sqrt{2}$)2,
∴△ABC是直角三角形.
故答案为:直角.
点评 本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.化简$\frac{-36}{-12}$的结果是( )
| A. | 3 | B. | -3 | C. | -4 | D. | 24 |
20.如图,将四根长度相等的细木条首尾相接钉成四边形ABCD,当∠B=90°时,测得AC=4,改变它的形状使∠B=60°,此时AC的长度为( )
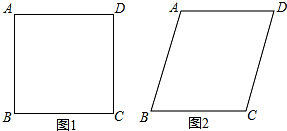

| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{6}$ | D. | 2$\sqrt{2}$ |
 仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米) ,tan48°≈
,tan48°≈ ,sin64°≈
,sin64°≈ ,tan64°≈2)
,tan64°≈2)
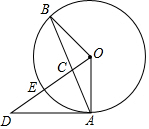 如图,A、B是⊙O上的两点,过O作OB的垂线交AB于C,交⊙O于E,交⊙O的切线AD于D.
如图,A、B是⊙O上的两点,过O作OB的垂线交AB于C,交⊙O于E,交⊙O的切线AD于D.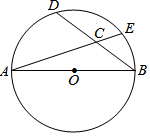 如图,AB是⊙O的直径,点D是弧AE的中点,AB=5,BD=4,则sin∠ECB=$\frac{4}{5}$.
如图,AB是⊙O的直径,点D是弧AE的中点,AB=5,BD=4,则sin∠ECB=$\frac{4}{5}$.