题目内容
13．
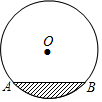如图，是一圆柱形输水管的横截面，半径为5cm，阴影部分为有水部分，如果水面AB宽为8cm，水面最深地方的高度为2cm．
分析 根据题意可得出AO=5cm，AC=4cm，由勾股定理得出CO的长，则CD=OD-OC=AO-OC．
解答 
解：如图所示：过O作OE⊥AB交⊙O于C，
∵输水管的半径为5cm，水面宽AB为8cm，水的最大深度为CE，
∴EO⊥AB，
∴AO=5cm，AC=4cm，
∴CO=$\sqrt{{5}^{2}-{4}^{2}}$=3（cm），
∴水的最大深度CE为：CE=OC-OE=AO-OE=2cm．
故答案是：2．
点评 本题考查的是垂径定理的应用及勾股定理，根据题意构造出直角三角形是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
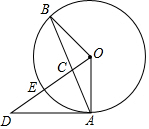如图，A、B是⊙O上的两点，过O作OB的垂线交AB于C，交⊙O于E，交⊙O的切线AD于D．
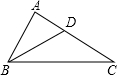如图，在△ABC中，∠A=90°，BD平分∠ABC，∠C=30°，AD=2，AB=2$\sqrt{3}$，那么S△ABC=6$\sqrt{3}$．
8．关于x的一元二次方程（m-1）x2+2mx+m=0有实数根，则m的取值范围是（ ）
| A． | x≥0 | B． | x≥0且≠1 | C． | m≠1 | D． | m＞1 |
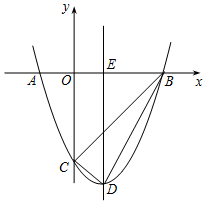如图，抛物线y=x2+bx+c与x轴交于A（-1，0）和B（3，0）两点，与y轴交于点C，对称轴与x轴交于点E，点D为顶点，连接BD、CD、BC．