题目内容
12.已知C为线段AB的中点,E为线段AB上的点,点D为线段AE的中点.(1)若线段AB=a,CE=b,|a-15|+(b-4.5)2=0|a-15|+(b-4.5)2=0,求a,b的值;

(2)如图1,在(1)的条件下,求线段DE的长;
(3)如图2,若AB=15,AD=2BE,求线段CE的长.
分析 (1)由|a-15|+(b-4.5)2=0,根据非负数的性质即可推出a、b的值;
(2)根据(1)所推出的结论,即可推出AB和CE的长度,根据图形即可推出AC=7.5,然后由AE=AC+CE,即可推出AE的长度,由D为AE的中点,即可推出DE的长度;
(3)首先设EB=x,根据线段中点的性质推出AD、DE关于x的表达式,即AD=DE=2x,由图形推出AD+DE+BE=15,即可得方程:x+2x+2x=15,通过解方程推出x=3,即BE=3,最后由BC=7.5,即可求出CE的长度.
解答 解:(1)∵|a-15|+(b-4.5)2=0,
∴|a-15|=0,(b-4.5)2=0,
∵a、b均为非负数,
∴a=15,b=4.5,
(2)∵点C为线段AB的中点,AB=15,CE=4.5,
∴AC=$\frac{1}{2}$AB=7.5,
∴AE=AC+CE=12,
∵点D为线段AE的中点,
∴DE=$\frac{1}{2}$AE=6,
(3)设EB=x,则AD=2BE=2x,
∵点D为线段AE的中点,
∴AD=DE=2x,
∵AB=15,
∴AD+DE+BE=15,
∴x+2x+2x=15,
解方程得:x=3,即BE=3,
∵AB=15,C为AB中点,
∴BC=$\frac{1}{2}$AB=7.5,
∴CE=BC-BE=7.5-3=4.5.
点评 本题主要考查线段中点的性质,关键在于正确的进行计算,熟练运用数形结合的思想推出相关线段之间的数量关系.

练习册系列答案
相关题目
7.在实数-$\sqrt{2}$,$\frac{π}{3}$,$\frac{1}{7}$,0.80108,$\sqrt{4}$,0.$\stackrel{•}{3}$$\stackrel{•}{1}$中无理数的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.一元一次方程-2x=4的解是( )
| A. | x=-2 | B. | x=2 | C. | x=1 | D. | x=-$\frac{1}{2}$ |
2.小红同学四次数学测试成绩分别是:96,104,104,116,关于这组数据下列说法错误的是( )
| A. | 平均数是105 | B. | 众数是104 | C. | 中位数是104 | D. | 方差是50 |
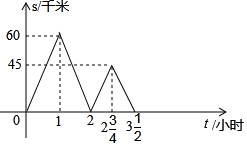 甲、乙两车沿同一平直公路由A地匀速行驶(中途不停留),前往终点B地,甲、乙两车之间的距离S(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.下列说法:
甲、乙两车沿同一平直公路由A地匀速行驶(中途不停留),前往终点B地,甲、乙两车之间的距离S(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.下列说法: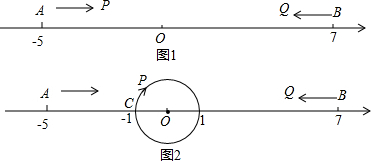
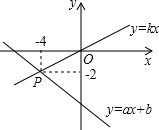 如图所示,已知函数y=ax+b和y=kx的图象相交于点P,则根据图象可得关于x,y的二元一次方程组$\left\{\begin{array}{l}y=ax+b\\ y=kx\end{array}$的解是$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$.
如图所示,已知函数y=ax+b和y=kx的图象相交于点P,则根据图象可得关于x,y的二元一次方程组$\left\{\begin{array}{l}y=ax+b\\ y=kx\end{array}$的解是$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$. 从2016年1月1日开始,北京市居民生活用气阶梯价格制度正式实施,一般生活用气收费标准如下表所示,比如6口以下的户年天然气用量在第二档时,其中350立方米按2.28元/m3收费,超过350立方米的部分按2.5元/m3收费.小锋一家有五口人,他想帮父母计算一下实行阶梯价后,家里天然气费的支出情况.
从2016年1月1日开始,北京市居民生活用气阶梯价格制度正式实施,一般生活用气收费标准如下表所示,比如6口以下的户年天然气用量在第二档时,其中350立方米按2.28元/m3收费,超过350立方米的部分按2.5元/m3收费.小锋一家有五口人,他想帮父母计算一下实行阶梯价后,家里天然气费的支出情况.