题目内容
1.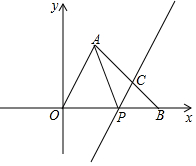 如图,将△OAB放在平面直角坐标系中,O为原点,点A(2,4),点B(6,0)在边OB上有一动点P,过P作PC∥OA交AB于C,连接AP.
如图,将△OAB放在平面直角坐标系中,O为原点,点A(2,4),点B(6,0)在边OB上有一动点P,过P作PC∥OA交AB于C,连接AP.(Ⅰ)求△OAB的面积;
(Ⅱ)若设OP=x,△APC的面积为y,试用含x的式子表示y;
(Ⅲ)若有满足S△APC=$\frac{1}{m}$S△OAB的点P存在,求当m取得最小值时,点P的坐标(直接写出结果即可).
分析 (1)先确定出AD和OB的长,最后用三角形的面积公式即可;
(2)先设出C的坐标,进而表示出BC,再用相似三角形的性质即可得出CE,最后用三角形的面积的差即可得出结论;
(3)借助(1)(2)得出结论,先确定出y的最大值,即可判断出m的最小值,进而求出点P的坐标.
解答 解:(1)如图1,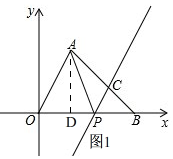 过点A作AD⊥x轴于D,
过点A作AD⊥x轴于D,
∵A(2,4),
∴AD=4,
∵B(6,0),
∴OB=6,
∴S△OAB=$\frac{1}{2}$OB×AD=$\frac{1}{2}$×6×4=12,
(2)如图2,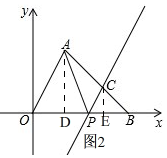 过点A作AD⊥x轴于D,过点C作CE⊥x轴,
过点A作AD⊥x轴于D,过点C作CE⊥x轴,
∵A(2,4),B(6,0),
∴直线AB的解析式为y=-x+6,
设C(a,-a+6)(0<a<6),
在Rt△ABD中,AD=4,BD=OB-OD=6-2=4,
∴tan∠OBA=$\frac{AD}{BD}$=1,
在Rt△BCE中,tan∠OBA=$\frac{CE}{BE}$=1,
∴BE=CE=-a+6,
∴BC=$\sqrt{2}$BE=$\sqrt{2}$(-a+6),
∵A(2,4),B(6,0),
∴AB=4$\sqrt{2}$,
∵PC∥OA,
∴△BPC∽△BOA,
∴$\frac{BC}{AB}=\frac{BP}{OB}$,
∵OP=x,OB=6,
∴BP=6-x,
∴$\frac{\sqrt{2}(-a+6)}{4\sqrt{2}}=\frac{6-x}{6}$,
∴a=2+$\frac{2}{3}$x,
∴CE=-a+6=-2-$\frac{2}{3}$x+6=4-$\frac{2}{3}$x,
∴y=S△ACP=S△OAB-S△OAP-S△BPC=12-$\frac{1}{2}$x×4-$\frac{1}{2}$(6-x)×(4-$\frac{2}{3}$x)=-$\frac{1}{3}$x2+2x(0<x<6),
(3)由(2)知,S△ACP=y=-$\frac{1}{3}$x2+2x=-$\frac{1}{3}$(x-3)2+3,
当x=3时,y最大=3
由(1)知,S△AOB=12,
∵S△APC=$\frac{1}{m}$S△OAB,
∴$\frac{12}{m}$的最大值为3,
∴m的最小值为4,
∴m最小时,P(3,0).
点评 此题是三角形的综合题,主要考查了三角形的面积公式,锐角三角函数的定义,相似三角形的判定和性质,解(2)的关键是确定出△PBC的边BP上的高,是一道基础题目.

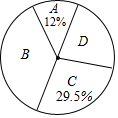 某区为了解七年级学生开展跳绳活动的情况,随机调查了该区部分学校七年级学生1分钟跳绳的次数,将调查结果进行统计,下面是根据调查数据制作的统计图表的一部分.
某区为了解七年级学生开展跳绳活动的情况,随机调查了该区部分学校七年级学生1分钟跳绳的次数,将调查结果进行统计,下面是根据调查数据制作的统计图表的一部分.| 分组 | 次数x(个) | 人数 |
| A | 0≤x<120 | 24 |
| B | 120≤x<130 | 72 |
| C | 130≤x<140 | |
| D | x≥140 |
(1)在被调查的学生中,跳绳次数在120≤x<130范围内的人数为72人,跳绳次数在0≤x<120范围内的人数占被调查人数的百分比为12%;
(2)本次共调查了200名学生,其中跳绳次数在130≤x<140范围内的人数为59人,跳绳次数在x≥140范围内的人数占被调查人数的百分比为22.5%;
(3)该区七年级共有4000名学生,估计该区七年级学生1分钟跳绳的次数不少于130个的人数.
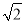 )2+|1﹣tanB|=0,则△ABC一定是( )
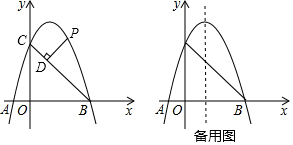
)2+|1﹣tanB|=0,则△ABC一定是( )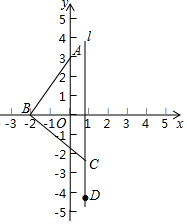 如图,已知在平面直角坐标系中,点A(0,3),点B为x轴上一动点,连接AB,线段AB绕着点B按顺时针方向旋转90°至线段CB,过点C作直线l∥y轴,在直线l上有一点D位于点C下方,满足CD=BO,则当点B从(-3,0)平移到(3,0)的过程中,点D的运动路径长为3+3$\sqrt{5}$.
如图,已知在平面直角坐标系中,点A(0,3),点B为x轴上一动点,连接AB,线段AB绕着点B按顺时针方向旋转90°至线段CB,过点C作直线l∥y轴,在直线l上有一点D位于点C下方,满足CD=BO,则当点B从(-3,0)平移到(3,0)的过程中,点D的运动路径长为3+3$\sqrt{5}$.
 在正方形ABCD中,点E在BC的延长线上,且CE=CD,点F为DE边上一点,连接AF,作FG⊥AF交直线DC于点G
在正方形ABCD中,点E在BC的延长线上,且CE=CD,点F为DE边上一点,连接AF,作FG⊥AF交直线DC于点G