题目内容
5.为了保护学生的视力,课桌的高度)ycm与椅子的高度xcm(不含靠背)都是按y是x的一次函数关系配套设计的,如表列出了两套课桌椅的高度:| 第一套 | 第二套 | |
| 椅子高度xcm | 40.0 | 38.0 |
| 课桌高度ycm | 75.0 | 71.8 |
(2)现有一把高42.0cm的椅子和一张高79.8cm的课桌,它们是否配套?请通过计算说明理由.
分析 (1)根据题意和表格中的数据可以计算出y与x的函数关系式;
(2)将x=42.0代入(1)中的函数解析式,然后与79.8作比较,即可解答本题.
解答 解:(1)设y=kx+b,
$\left\{\begin{array}{l}{75=40k+b}\\{71.8=38k+b}\end{array}\right.$,得$\left\{\begin{array}{l}{k=1.6}\\{b=11}\end{array}\right.$,
即y与x的函数关系式是y=1.6x+11;
(2)现有一把高42.0cm的椅子和一张高79.8cm的课桌,它们不配套,
理由:当x=42.0时,y=1.6×42.0+11=78.2,
∵78.2≠79.8,
∴现有一把高42.0cm的椅子和一张高79.8cm的课桌,它们不配套.
点评 本题考查一次函数的应用,解答此类问题的关键是明确题意,求出相应的函数解析式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.在Rt△ABC中,∠C=90°,AB=15,sinA=$\frac{1}{3}$,则BC=( )
| A. | 5 | B. | 10$\sqrt{2}$ | C. | 45 | D. | $\frac{1}{5}$ |
10. 实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
 实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )| A. | a-c>b-c | B. | $\frac{a}{b}$<$\frac{c}{b}$ | C. | ac>bc | D. | a+c<b+c |
17.在某次聚会上,每两人都握了一次手,所有人共握了10次,设有x人参加这次聚会,则列出方程正确的是( )
| A. | x(x+1)=10 | B. | $\frac{x(x+1)}{2}$=10 | C. | x(x-1)=10 | D. | $\frac{x(x-1)}{2}$=10 |
14.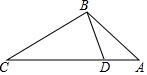 如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )
如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )
 如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )
如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )| A. | ∠ABD=∠C | B. | ∠ADB=∠ABC | C. | $\frac{AB}{BD}=\frac{CB}{CA}$ | D. | $\frac{AB}{AD}=\frac{AC}{AB}$ |
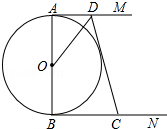 如图,AB是⊙O的直径,AM、BN分别与⊙O相切于点A、B,CD交AM、BN于点D、C,DO平分∠ADC.
如图,AB是⊙O的直径,AM、BN分别与⊙O相切于点A、B,CD交AM、BN于点D、C,DO平分∠ADC.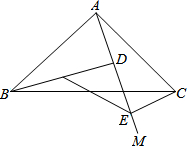 如图,在△ABC中,∠BAC=90°,AB=AC,AM是过点A的任意一条直线,BD⊥AM于点D,CE⊥AM于点E,求证:DE=BD-CE.
如图,在△ABC中,∠BAC=90°,AB=AC,AM是过点A的任意一条直线,BD⊥AM于点D,CE⊥AM于点E,求证:DE=BD-CE. 如图是二次函数y1=ax2+bx+c(a≠0)和一次函数y2=kx+t的图象,当y1≥y2时,x的取值范围是-1≤x≤2.
如图是二次函数y1=ax2+bx+c(a≠0)和一次函数y2=kx+t的图象,当y1≥y2时,x的取值范围是-1≤x≤2.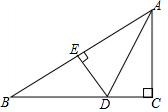 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,AC=3,BC=4.
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,AC=3,BC=4.