题目内容
15.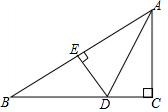 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,AC=3,BC=4.
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,AC=3,BC=4.(1)求DE的长;
(2)求△ADB的面积.
分析 (1)根据角平分线的性质可得DE=CD,证明Rt△AED≌Rt△ACD可得AE=AC,再利用勾股定理计算出AB长,进而可得BE的长,然后设DE=x,则CD=x,BC=4-x,利用勾股定理列出方程,再解即可;
(2)计算出BD的长,利用三角形面积公式可得答案.
解答 解:(1)∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴DE=CD,
在Rt△AED和Rt△ADC中$\left\{\begin{array}{l}{ED=CD}\\{AD=AD}\end{array}\right.$,
∴Rt△AED≌Rt△ACD(HL),
∴AE=AC=3,
∵AC=3,BC=4,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴EB=5-3=2,
设DE=x,则CD=x,BC=4-x,
x2+22=(4-x)2,
解得:x=1.5,
则DE=1.5;
(2)∵DE=1.5,
∴CD=1.5,
∴BD=2.5,
∴△ADB的面积:$\frac{1}{2}×$2.5×3=$\frac{15}{4}$.
点评 此题主要考查了勾股定理的应用,以及角平分线的性质,关键是掌握角的平分线上的点到角的两边的距离相等.

练习册系列答案
相关题目
5.为了保护学生的视力,课桌的高度)ycm与椅子的高度xcm(不含靠背)都是按y是x的一次函数关系配套设计的,如表列出了两套课桌椅的高度:
(1)请确定y与x的函数关系式(不要求写出x的取值范围);
(2)现有一把高42.0cm的椅子和一张高79.8cm的课桌,它们是否配套?请通过计算说明理由.
| 第一套 | 第二套 | |
| 椅子高度xcm | 40.0 | 38.0 |
| 课桌高度ycm | 75.0 | 71.8 |
(2)现有一把高42.0cm的椅子和一张高79.8cm的课桌,它们是否配套?请通过计算说明理由.
6. 如图,在4×4的网格中,将△ABC绕B顺时针旋转90°得到△BDE,则A走过的路径的长是( )
如图,在4×4的网格中,将△ABC绕B顺时针旋转90°得到△BDE,则A走过的路径的长是( )
 如图,在4×4的网格中,将△ABC绕B顺时针旋转90°得到△BDE,则A走过的路径的长是( )
如图,在4×4的网格中,将△ABC绕B顺时针旋转90°得到△BDE,则A走过的路径的长是( )| A. | π | B. | 2π | C. | 3π | D. | 1.5π |
3.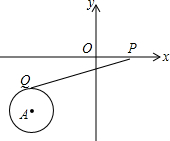 如图,点A的坐标为(-3,-2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小值时,点P的坐标为( )
如图,点A的坐标为(-3,-2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小值时,点P的坐标为( )
 如图,点A的坐标为(-3,-2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小值时,点P的坐标为( )
如图,点A的坐标为(-3,-2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小值时,点P的坐标为( )| A. | (-4,0) | B. | (-2,0) | C. | (-4,0)或(-2,0) | D. | (-3,0) |
10.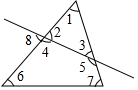 如图,按各角的位置,下列判断错误的是( )
如图,按各角的位置,下列判断错误的是( )
 如图,按各角的位置,下列判断错误的是( )
如图,按各角的位置,下列判断错误的是( )| A. | ∠5与∠8是同位角 | B. | ∠5与∠6是同旁内角 | ||
| C. | ∠3与∠4是内错角 | D. | ∠1与∠2是同旁内角 |
20.下列图案中,不是轴对称图形的个数是( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
7.在下列坐标平面内的各点中,在x轴上的点是( )
| A. | (-1,0) | B. | (0,1) | C. | (-1,2) | D. | (-2,-1) |
4.2016年10月17日早晨7:30:28,中国的载人航天飞船神州十一号由长征2F摇十一火箭发射升空,神州十一号飞船成功飞向浩瀚宇宙,并在距地面约390000米的轨道上与天宫二号交会对接,将390000用科学记数法表示应为( )
| A. | 3.9×104 | B. | 3.9×105 | C. | 39×104 | D. | 0.39×106 |
5.若|a|=4,|b|=5,且ab<0,则a+b的值是( )
| A. | 1 | B. | -9 | C. | 9或-9 | D. | 1或-1 |