题目内容
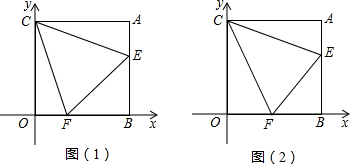
如图(1),在平面直角坐标系中,点A(n,m)在第一象限,AB⊥x轴于B,AC⊥y轴于C,(m-3)2+n2=6n-9,过C点作∠ECF分别交线段AB、OB于E、F两点.
(1)求m、n的值并写出A、B、C三点的坐标;
(2)若OF+BE=AB,求证:CF=CE;
(3)如图(2),若∠ECF=45°,给出两个结论:①OF+AE-EF的值不变; ②OF+AE+EF的值不变,其中有且只有一个结论正确,请你判断出正确的结论,并加以证明.
(1)求m、n的值并写出A、B、C三点的坐标;
(2)若OF+BE=AB,求证:CF=CE;
(3)如图(2),若∠ECF=45°,给出两个结论:①OF+AE-EF的值不变; ②OF+AE+EF的值不变,其中有且只有一个结论正确,请你判断出正确的结论,并加以证明.

考点:四边形综合题
专题:综合题
分析:(1)已知等式变形后,利用非负数的性质求出m与n的值,即可确定出A,B,C的坐标;
(2)由AE+EB=AB,以及OF+BE=AB,得到AE=OF,根据四边形ABOC为正方形,得到CA=CO,且∠A=∠COF=90°,利用SAS得到三角形ACE与三角形OCF全等,利用全等三角形对应边相等得到CF=CE;
(3)结论①正确,即OF+AE-EF的值不变,理由为:在x轴负半轴上取点H,使OH=AE,连接CH,利用SAS得到三角形ACE与三角形OCH全等,利用全等三角形对应边相等得到EC=HC,∠1=∠2,根据∠ACO=90°,∠ECF=45°,得到∠1+∠3=45°,等量代换得到∠2+∠3=45°,即∠ECF=∠HCF,利用SAS得到三角形ECF与三角形HCF全等,利用全等三角形对应边相等得到EF=HF,而HF=OH+OF,等量代换得到EF=AE+OF,即AE+OF-EF=0.
(2)由AE+EB=AB,以及OF+BE=AB,得到AE=OF,根据四边形ABOC为正方形,得到CA=CO,且∠A=∠COF=90°,利用SAS得到三角形ACE与三角形OCF全等,利用全等三角形对应边相等得到CF=CE;
(3)结论①正确,即OF+AE-EF的值不变,理由为:在x轴负半轴上取点H,使OH=AE,连接CH,利用SAS得到三角形ACE与三角形OCH全等,利用全等三角形对应边相等得到EC=HC,∠1=∠2,根据∠ACO=90°,∠ECF=45°,得到∠1+∠3=45°,等量代换得到∠2+∠3=45°,即∠ECF=∠HCF,利用SAS得到三角形ECF与三角形HCF全等,利用全等三角形对应边相等得到EF=HF,而HF=OH+OF,等量代换得到EF=AE+OF,即AE+OF-EF=0.
解答: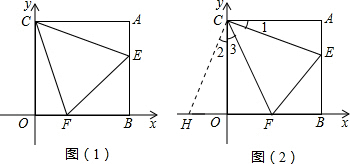 解:(1)将(m-3)2+n2=6n-9变形得:(m-3)2+(n-3)2=0,
解:(1)将(m-3)2+n2=6n-9变形得:(m-3)2+(n-3)2=0,
∴m=3,n=3,
∴A(3,3),B(3,0),C(0,3);
(2)∵OF+BE=AB,AE+EB=AB,
∴AE=OF,
∵四边形ABCD为正方形,
∴AC=OC,∠A=∠COF=90°,
在△ACE和△OCF中,
,
∴△ACE≌△OCF(SAS),
∴CF=CE;
(3)结论①正确,即OF+AE-EF的值不变,理由为:
在x轴负半轴上取点H,使OH=AE,连接CH,
∵四边形ABCD为正方形,
∴AC=OC,∠A=∠COH=90°,
在△ACE和△OCH中,
,
∴△ACE≌△OCH(SAS),
∴∠1=∠2,EC=HC,
∵∠ACO=90°,∠ECF=45°,
∴∠1+∠3=45°,
∴∠2+∠3=45°,即∠ECF=∠HCF,
在△ECF和△HCF中,
,
∴△ECF≌△HCF(SAS),
∴EF=HF=HO+OF=AE+OF,
则OF+AE-EF=0.
 解:(1)将(m-3)2+n2=6n-9变形得:(m-3)2+(n-3)2=0,
解:(1)将(m-3)2+n2=6n-9变形得:(m-3)2+(n-3)2=0,∴m=3,n=3,
∴A(3,3),B(3,0),C(0,3);
(2)∵OF+BE=AB,AE+EB=AB,
∴AE=OF,
∵四边形ABCD为正方形,
∴AC=OC,∠A=∠COF=90°,
在△ACE和△OCF中,
|
∴△ACE≌△OCF(SAS),
∴CF=CE;
(3)结论①正确,即OF+AE-EF的值不变,理由为:
在x轴负半轴上取点H,使OH=AE,连接CH,
∵四边形ABCD为正方形,
∴AC=OC,∠A=∠COH=90°,
在△ACE和△OCH中,
|
∴△ACE≌△OCH(SAS),
∴∠1=∠2,EC=HC,
∵∠ACO=90°,∠ECF=45°,
∴∠1+∠3=45°,
∴∠2+∠3=45°,即∠ECF=∠HCF,
在△ECF和△HCF中,
|
∴△ECF≌△HCF(SAS),
∴EF=HF=HO+OF=AE+OF,
则OF+AE-EF=0.
点评:此题属于四边形综合题,涉及的知识有:坐标与图形性质,全等三角形的判定与性质,非负数的性质,正方形的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,AB∥CD,∠A=40°,∠C=45°,求∠D和∠AOC.
如图,AB∥CD,∠A=40°,∠C=45°,求∠D和∠AOC.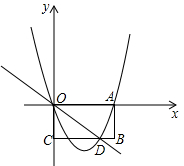 已知矩形OABC在平面直角坐标系中位置如图,点A的坐标为(6,0),点C的坐标为(0,-3),直线y=-
已知矩形OABC在平面直角坐标系中位置如图,点A的坐标为(6,0),点C的坐标为(0,-3),直线y=-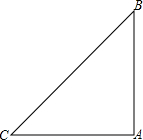 问题:已知△ABC中,∠BAC=2∠ACB,点D是△ABC内的一点,且AD=CD,BD=BA.当∠BAC=90°时:
问题:已知△ABC中,∠BAC=2∠ACB,点D是△ABC内的一点,且AD=CD,BD=BA.当∠BAC=90°时:
 如图,已知正方形ABCD的边长是2,点E在DC上,△ADE经顺时针旋转后与△ABF重合.
如图,已知正方形ABCD的边长是2,点E在DC上,△ADE经顺时针旋转后与△ABF重合.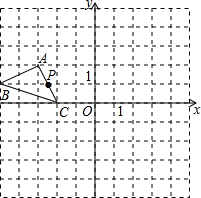 如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P1(a+6,b+2).
如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P1(a+6,b+2).