题目内容
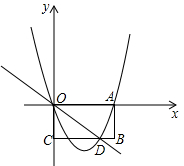 已知矩形OABC在平面直角坐标系中位置如图,点A的坐标为(6,0),点C的坐标为(0,-3),直线y=-
已知矩形OABC在平面直角坐标系中位置如图,点A的坐标为(6,0),点C的坐标为(0,-3),直线y=-| 3 |
| 4 |
(1)求点D的坐标.
(2)抛物线y=ax2+bx+c经过点A、D、O,求此抛物线的表达式.
(3)在这个抛物线上是否存在点M,使以O、D、A、M为顶点的四边形是梯形?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.
考点:二次函数综合题,待定系数法求一次函数解析式,待定系数法求二次函数解析式,矩形的性质,梯形
专题:综合题
分析:(1)由四边形OABC是矩形及点C的坐标可得点D的纵坐标,就可求出点D的坐标.
(2)用待定系数法就可求出抛物线的解析式.
(3)分别以OA、OD、AD为梯形的底边进行讨论,求出过点M的底边所在直线的解析式,然后求出该直线与抛物线的交点就是所求点M的坐标.
(2)用待定系数法就可求出抛物线的解析式.
(3)分别以OA、OD、AD为梯形的底边进行讨论,求出过点M的底边所在直线的解析式,然后求出该直线与抛物线的交点就是所求点M的坐标.
解答:解:(1)如图1,

∵四边形OABC是矩形,点C的坐标为(0,-3),
∴yD=yC=-3.
∴-
xD=-3.
解得:xD=4.
∴点D的坐标为(4,-3).
(2)∵点O(0,0)、点A(6,0)、点D(4,-3)在抛物线y=ax2+bx+c上,
∴
.
解得:
.
∴该抛物线的解析式为y=
x2-
x.
(3)①若OA为梯形的底边,如图2,

则有DM∥OA.
∴yM=yD=-3.
∴
xM2-
xM=-3.
解得:x1=2,x2=4.
∴点M的坐标为(2,-3).
②若OD为梯形的底边,如图3,

则有AM∥OD.
设AM的解析式为y=-
x+b,
则有-
×6+b=0.
解得:b=
.
∴AM的解析式为y=-
x+
.
联立
解得:
或
∴点M的坐标为(-2,6).
③若AD为梯形的底边,如图4,

则有OM∥AD.
同理可得:点M的坐标为(10,15).
综上所述:符合条件的点M的坐标为(2,-3)或(-2,6)或(10,15).

∵四边形OABC是矩形,点C的坐标为(0,-3),
∴yD=yC=-3.
∴-
| 3 |
| 4 |
解得:xD=4.
∴点D的坐标为(4,-3).
(2)∵点O(0,0)、点A(6,0)、点D(4,-3)在抛物线y=ax2+bx+c上,
∴
|
解得:
|
∴该抛物线的解析式为y=
| 3 |
| 8 |
| 9 |
| 4 |
(3)①若OA为梯形的底边,如图2,

则有DM∥OA.
∴yM=yD=-3.
∴
| 3 |
| 8 |
| 9 |
| 4 |
解得:x1=2,x2=4.
∴点M的坐标为(2,-3).
②若OD为梯形的底边,如图3,

则有AM∥OD.
设AM的解析式为y=-
| 3 |
| 4 |
则有-
| 3 |
| 4 |
解得:b=
| 9 |
| 2 |
∴AM的解析式为y=-
| 3 |
| 4 |
| 9 |
| 2 |
联立
|
解得:
|
|
∴点M的坐标为(-2,6).
③若AD为梯形的底边,如图4,

则有OM∥AD.
同理可得:点M的坐标为(10,15).
综上所述:符合条件的点M的坐标为(2,-3)或(-2,6)或(10,15).
点评:本题考查了用待定系数法求抛物线及直线的解析式、梯形的性质、抛物线与直线的交点、矩形的性质等知识,考查了分类讨论的思想,由一定的综合性.

练习册系列答案
相关题目
 如图,四边形OABC为矩形,OA=4,OC=5,正比例函数y=2x的图象交AB于点D,连接DC,动点Q从D点出发沿DC向终点C运动,动点P从C点出发沿CO向终点O运动.两点同时出发,速度均为每秒1个单位,设从出发起运动了ts.
如图,四边形OABC为矩形,OA=4,OC=5,正比例函数y=2x的图象交AB于点D,连接DC,动点Q从D点出发沿DC向终点C运动,动点P从C点出发沿CO向终点O运动.两点同时出发,速度均为每秒1个单位,设从出发起运动了ts.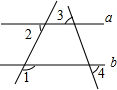 如图,a∥b,∠1=112°,∠3=50°,求∠2和∠4的度数.
如图,a∥b,∠1=112°,∠3=50°,求∠2和∠4的度数. 依据给定的条件,求一次函数的解析式.
依据给定的条件,求一次函数的解析式.