题目内容
8. 为了测量学校升旗杆AB的高度,班长小颖带领兴趣小组在距离旗发现标杆完全遮住了升旗杆,若小颖的眼睛E距地面高为1.5m,试求升旗杆AB的高度.
为了测量学校升旗杆AB的高度,班长小颖带领兴趣小组在距离旗发现标杆完全遮住了升旗杆,若小颖的眼睛E距地面高为1.5m,试求升旗杆AB的高度.
分析 过点E作EG∥BF,交CD于点H,交AB于点G,由△EHC∽△EGA,推出$\frac{EH}{EC}$=$\frac{CH}{AC}$,求出AG即可解决问题.
解答 解:过点E作EG∥BF,交CD于点H,交AB于点G,
则EH=FD=5 m,HG=BD=20 m,GB=HD=EF=1.5 m,CH=3=1.5=1.5(m),
∵CH∥AG,
∴△EHC∽△EGA,
∴$\frac{EH}{EC}$=$\frac{CH}{AC}$,
∴AG=7.5m
∴AB=AG+BG=7.5+1.5=9(m),即旗杆的高为9 m.
点评 本题考查相似三角形的应用、解题的关键是学会添加常用辅助线,构造相似三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
19.先化简,再求值:$\frac{a-b}{a+2b}$÷$\frac{{a}^{2}-{b}^{2}}{{a}^{2}+4ab+4{b}^{2}}$-1.其中a=$\sqrt{3}$-1,b=1.
18.现有一批水果包装质量为每筐25千克,现抽取8框样品进行检测,结果称重记录如下(单位:千克):27,24,25,28,21,26,22,27.为了求得8筐样品的总质量,我们可以选取一个恰当的基准数进行化简计算.
(1)请你选择一个恰当的基准数为25;
(2)根据你选的基准数,用正、负数填写下表:
(3)这8筐水果的总质量是多少?
(1)请你选择一个恰当的基准数为25;
(2)根据你选的基准数,用正、负数填写下表:
| 原质量 | 27 | 24 | 25 | 28 | 21 | 26 | 22 | 27 |
| 与基准数的差 | 2 | -1 | 0 | 3 | -4 | 1 | -3 | 2 |
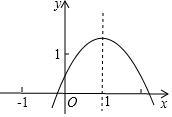 已知二次函数y=ax2+bx+c(a≠0)的对称轴是直线x=1,图象如图所示.给出下面五个结论:①abc>0;②2a+b=0;③b2-4ac>0;④a+b>m(am+b)(m为实数,且m≠1);⑤2c>3b.
已知二次函数y=ax2+bx+c(a≠0)的对称轴是直线x=1,图象如图所示.给出下面五个结论:①abc>0;②2a+b=0;③b2-4ac>0;④a+b>m(am+b)(m为实数,且m≠1);⑤2c>3b. 如图中大、小正方形的边长分别为a和2(a>2);
如图中大、小正方形的边长分别为a和2(a>2);