题目内容
19.先化简,再求值:$\frac{a-b}{a+2b}$÷$\frac{{a}^{2}-{b}^{2}}{{a}^{2}+4ab+4{b}^{2}}$-1.其中a=$\sqrt{3}$-1,b=1.分析 将分子、分母因式分解后,除法转化为乘法,再约分,继而计算减法即可化简原式,最后将a、b的值代入计算可得.
解答 解:原式=$\frac{a-b}{a+2b}$•$\frac{(a+2b)^{2}}{(a+b)(a-b)}$-1
=$\frac{a+2b}{a+b}$-$\frac{a+b}{a+b}$
=$\frac{b}{a+b}$,
当a=$\sqrt{3}$-1,b=1时,
原式=$\frac{1}{\sqrt{3}-1+1}$=$\frac{\sqrt{3}}{3}$.
点评 本题主要考查分式的化简求值,熟练掌握分式的混合运算顺序和运算法则是解题的关键.

练习册系列答案
相关题目
4.在解方程$\frac{x}{3}$=1-$\frac{x-1}{5}$时,去分母后正确的是( )
| A. | 5x=15-3(x-1) | B. | x=1-(3 x-1) | C. | 5x=1-3(x-1) | D. | 5 x=3-3(x-1) |
9. 如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠ABC=25°,则∠P的度数为( )
如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠ABC=25°,则∠P的度数为( )
 如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠ABC=25°,则∠P的度数为( )
如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠ABC=25°,则∠P的度数为( )| A. | 50° | B. | 40° | C. | 65° | D. | 55° |
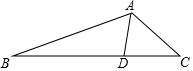 如图,在△ABC中,AB=6,AC=4,∠BAC=120°,∠BAC的平分线交BC于点D,则AD=$\frac{12}{5}$.
如图,在△ABC中,AB=6,AC=4,∠BAC=120°,∠BAC的平分线交BC于点D,则AD=$\frac{12}{5}$. 为了测量学校升旗杆AB的高度,班长小颖带领兴趣小组在距离旗发现标杆完全遮住了升旗杆,若小颖的眼睛E距地面高为1.5m,试求升旗杆AB的高度.
为了测量学校升旗杆AB的高度,班长小颖带领兴趣小组在距离旗发现标杆完全遮住了升旗杆,若小颖的眼睛E距地面高为1.5m,试求升旗杆AB的高度.