题目内容
3.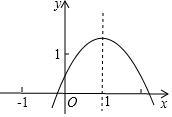 已知二次函数y=ax2+bx+c(a≠0)的对称轴是直线x=1,图象如图所示.给出下面五个结论:①abc>0;②2a+b=0;③b2-4ac>0;④a+b>m(am+b)(m为实数,且m≠1);⑤2c>3b.
已知二次函数y=ax2+bx+c(a≠0)的对称轴是直线x=1,图象如图所示.给出下面五个结论:①abc>0;②2a+b=0;③b2-4ac>0;④a+b>m(am+b)(m为实数,且m≠1);⑤2c>3b.其中正确的有②③④ (写出所有正确结论的序号).
分析 由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:①由图象可知:a<0,b>0,c>0,abc<0,错误;
②∵抛物线的对称轴x=-$\frac{b}{2a}$=1,
∴b=-2a,即2a+b=0,正确;
③∵抛物线与x轴有两个交点,
∴b2-4ac>0,正确;
④当x=1时,y的值最大.此时,y=a+b+c,
而当x=m≠1时,y=am2+bm+c,
所以a+b+c>am2+bm+c,
故a+b>am2+bm,即a+b>m(am+b),正确;
⑤当x=3时函数值小于0,y=9a+3b+c<0,且x=-$\frac{b}{2a}$=1,
即a=-$\frac{b}{2}$,代入得9(-$\frac{b}{2}$)+3b+c<0,得2c<3b,错误;
故答案为:②③④.
点评 本题主要考查二次函数图象与系数的关系,掌握二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴和、抛物线与y轴的交点、抛物线与x轴交点的个数确定是解题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
13.一个三角形的周长为7cm,一边长为3cm,其中有两条边的长度相等,则这个三角形的各边长是( )
| A. | 3 cm,2 cm,2 cm | |
| B. | 3 cm,1 cm,3 cm | |
| C. | 3 cm,2 cm,2 cm和3 cm,1 cm,3 cm都有可能 | |
| D. | 不能确定 |
13.已知方程(a-2)x|a|-1+3=0是关于x的一元一次方程,则a=( )
| A. | ±2 | B. | 1 | C. | 2 | D. | -2 |
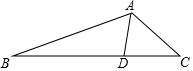 如图,在△ABC中,AB=6,AC=4,∠BAC=120°,∠BAC的平分线交BC于点D,则AD=$\frac{12}{5}$.
如图,在△ABC中,AB=6,AC=4,∠BAC=120°,∠BAC的平分线交BC于点D,则AD=$\frac{12}{5}$. 为了测量学校升旗杆AB的高度,班长小颖带领兴趣小组在距离旗发现标杆完全遮住了升旗杆,若小颖的眼睛E距地面高为1.5m,试求升旗杆AB的高度.
为了测量学校升旗杆AB的高度,班长小颖带领兴趣小组在距离旗发现标杆完全遮住了升旗杆,若小颖的眼睛E距地面高为1.5m,试求升旗杆AB的高度.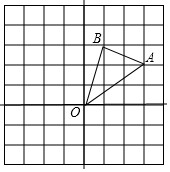 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1.