题目内容
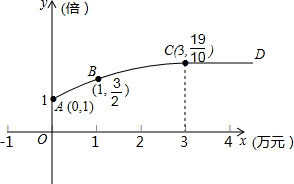 某公司生产一种产品,每件成本3元,售价4元,年销售量20万件,为获得更好的效益,公司准备拿出一定资金做广告.根据经验,设广告费x万元,做广告后的年销售量是原销售量的y倍,且y与x的关系如图所示,图中ABC为抛物线一段,CD为一条平行于x轴的射线,如果把利润看成是销售总额减去成本费和广告费
某公司生产一种产品,每件成本3元,售价4元,年销售量20万件,为获得更好的效益,公司准备拿出一定资金做广告.根据经验,设广告费x万元,做广告后的年销售量是原销售量的y倍,且y与x的关系如图所示,图中ABC为抛物线一段,CD为一条平行于x轴的射线,如果把利润看成是销售总额减去成本费和广告费(1)求y与x的函数关系式;
(2)试比较广告费分别为2.5万元和3.5万元时,产品销售售量的大小;
(3)求出利润s(万元)与广告费x(万元)之间的函数关系式及获得最大利润时投入的广告费是多少?
考点:二次函数的应用
专题:
分析:(1)由图象可知y与x的函数关系式为分段函数:当0≤x<3时为二次函数,当x≥3时为平行于x轴的一条直线;
(2)根据已知条件直接求出广告费分别为2.5万元和3.5万元时,产品销售售量;
(3)根据年利润S=原年销售量×x×每件产品的利润-广告费,把相关数值代入求得不同范围的年利润即可.
(2)根据已知条件直接求出广告费分别为2.5万元和3.5万元时,产品销售售量;
(3)根据年利润S=原年销售量×x×每件产品的利润-广告费,把相关数值代入求得不同范围的年利润即可.
解答:解:(1)当0≤x<3时,设函数解析式为:
y=ax2+bx+c,把点A(0,1),B(1,
),C(3,
)代入得,
,
解得
.
故函数解析式为y=-0.1x2+0.6x+1;
当x≥3时,函数解析式为:y=1.9;
(2)当x=2.5时,销售量为:20×(-0.1×2.52+0.6×2.5+1)=20×1.875=37.5(万件);
当x=3.5时,销售量为:20×1.9=38(万件);
(3)当0≤x<3时,
S=(4-3)×20y-x=-2x2+11x+20=-2(x-
)2+
,
当x=
时,S最大为
;
当x≥3时,
S=(4-3)×20y-x=38-x,
当x=3时,S最大为35,
∵
>35,
∴当x=
时,S最大为
;
即当广告费为2.75万元时,所获利润最大为35.125万元.
y=ax2+bx+c,把点A(0,1),B(1,
| 3 |
| 2 |
| 19 |
| 10 |
|
解得
|
故函数解析式为y=-0.1x2+0.6x+1;
当x≥3时,函数解析式为:y=1.9;
(2)当x=2.5时,销售量为:20×(-0.1×2.52+0.6×2.5+1)=20×1.875=37.5(万件);
当x=3.5时,销售量为:20×1.9=38(万件);
(3)当0≤x<3时,
S=(4-3)×20y-x=-2x2+11x+20=-2(x-
| 11 |
| 4 |
| 281 |
| 8 |
当x=
| 11 |
| 4 |
| 281 |
| 8 |
当x≥3时,
S=(4-3)×20y-x=38-x,
当x=3时,S最大为35,
∵
| 281 |
| 8 |
∴当x=
| 11 |
| 4 |
| 281 |
| 8 |
即当广告费为2.75万元时,所获利润最大为35.125万元.
点评:此题主要考查了二次函数的应用;理解题意,利用待定系数法求函数解析式以及得到利润的关系式是解决本题的关键.

练习册系列答案
相关题目
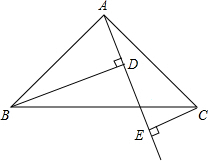 如图,Rt△ABC中,AB=AC,∠BAC=90°,直线AE是经过点A的任一直线,BD⊥AE于D,CE⊥AE于E,若BD>CE,试问:
如图,Rt△ABC中,AB=AC,∠BAC=90°,直线AE是经过点A的任一直线,BD⊥AE于D,CE⊥AE于E,若BD>CE,试问: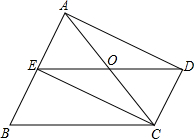 已知:如图,DC∥AB,且DC=AE,E为AB的中点,
已知:如图,DC∥AB,且DC=AE,E为AB的中点,