题目内容
10.已知二次函数y=(x-1)(x-a-1)(a为常数,且a>0).(1)求证:不论a为何值,该二次函数的图象总经过x轴上一定点;
(2)设该函数图象与x轴的交点为A、B(点A在点B的左侧),与y轴的交点为C,△ABC的面积为1.
①求a的值;
②D是该函数图象上一点,且点D的横坐标是m,若S△ABD=$\frac{1}{8}$S△ABC,直接写出m的值.
分析 (1)令y=0可求得对应方程的两根,可求得二次函数与x轴的交点,可证得结论;
(2)①结合(1)可用a表示出AB、OC,从而可表示出△ABC的面积,可求得a的值;②由①可得到抛物线的解析式,用m表示出D到AB的距离,可表示出△ABD的面积,可得到关于m的方程,可求得m的值.
解答 (1)证明:
令y=0,则(x-1)(x-a-1)=0.
解得x1=1,x2=1+a.
∴二次函数的图象与x轴的交点为(1,0)、(1+a,0).
∴不论a为何值,该二次函数的图象经过x轴上的定点(1,0).
(2)解:
①由题意得,AB=a,OC=1+a(a>0),
∴S△ABC=$\frac{1}{2}$AB•OC=$\frac{1}{2}$a(a+1).
∴$\frac{1}{2}$a(a+1)=1.
解得a1=1,a2=-2(舍去).
∵a>0,
∴a=1.
②由①可得抛物线为y=x2-3x+2,
令y=0可得0=x2-3x+2,解得x=1或x=2,
∴AB=1,
由于D点在抛物线上,故可设D点坐标为(m,m2-3m+2),
∴D到AB的距离为h=|m2-3m+2|,且S△ABC=1,
∴S△ABD=$\frac{1}{2}$AB•h=$\frac{1}{2}$×1×|m2-3m+2|=$\frac{1}{8}$,
整理可得|m2-3m+2|=$\frac{1}{4}$,
当m2-3m+2=$\frac{1}{4}$时,解得m=$\frac{3±\sqrt{2}}{2}$,当m2-3m+2=-$\frac{1}{4}$时,解得m=$\frac{3}{2}$,
∴m的值为$\frac{3+\sqrt{2}}{2}$或$\frac{3-\sqrt{2}}{2}$或$\frac{3}{2}$.
点评 本题主要考查二次函数与x轴的交点,掌握二次函数与x轴的交点横坐标是对应一元二次方程的两根是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 6cm | B. | 5cm | C. | $\sqrt{5}$cm | D. | 7.5cm |
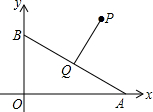 如图,点A、B分别在x轴和y轴的正半轴上运动,在运动过程中保持AB=4不变,点Q为AB的中点,已知点P的坐标为(4,3),连结PQ,则PQ长的最小值是3.
如图,点A、B分别在x轴和y轴的正半轴上运动,在运动过程中保持AB=4不变,点Q为AB的中点,已知点P的坐标为(4,3),连结PQ,则PQ长的最小值是3.
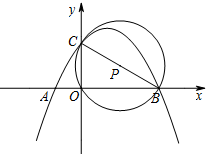 如图,抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,$\sqrt{3}$)三点.
如图,抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,$\sqrt{3}$)三点.