题目内容
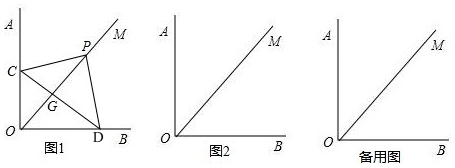
14.已知平面上有两条直线AB和CD,E是平面上该两直线处一点.(1)如图1,若直线AB∥CD,∠ABE=40°,∠CDE=25°,则∠BED=65°;
(2)若将E点移至图2所示位置,且∠ABE+∠CDE+∠BED=360°,则AB与CD的位置关系是AB∥CD;请说明理由.
(3)探索:如图3,在(1)的基础上,再增加两个拆点,则∠1、∠2、∠3、∠4、∠5的关系是∠1+∠2+∠4=∠5+∠3;
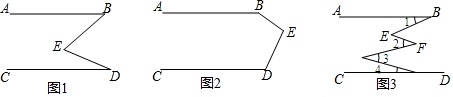
分析 (1)过点E作EF∥AB,根据平行公理可得EF∥CD,然后利用两直线平行,内错角相等可得∠1=∠ABE,∠2=∠CDE,然后根据∠BED=∠1+∠2计算即可得解;
(2)连接BD,根据三角形内角和定理得出∠E+∠EDB+∠EBD=180°,求出∠ABD+∠CDB=180°,根据平行线的判定推出即可;
(3)同理依据两直线平行,内错角相等即可证得∠1+∠2+∠4=∠5+∠3.
解答 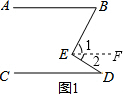 解:(1)如图1,过点E作EF∥AB,
解:(1)如图1,过点E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠1=∠ABE,∠2=∠CDE,
∴∠BED=∠1+∠2=40°+25°=65°,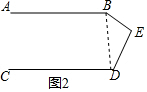
故答案为:65°;
(2)AB∥CD,
理由:连接BD,
∵∠ABE+∠E+∠CDE=360°,∠E+∠EDB+∠EBD=180°,
∴∠ABD+∠CDB=180°,
∴AB∥CD;
故答案为:AB∥CD;
(3)由(1)的结论得,∠1+∠2+∠4=∠5+∠3,
故答案为:∠1+∠2+∠4=∠5+∠3.
点评 本题考查了平行线性质的应用,关键是正确作辅助线,利用性质解决问题.

练习册系列答案
相关题目
5.有以下5个说法:①两点之间,线段最短:②相等的角是对顶角:③互补的两个角中必定一个是锐角一个钝角;④两个说角的和一定是锐角:⑤同角或等角的余角相等.其中正确的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
9.一次函数y=2x+1的图象不经过( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
19.有研究发现,人体在注射一定剂量的某种药物后的数小时内,体内血液中的药物浓度(即血药浓度)y毫克/升是时间t(小时)的二次函数,已知某病人的三次化验结果如表:
(1)求y与t的函数关系式;
(2)在注射后的第几小时,该病人体内的血药浓度达到最大?最大浓度是多少?
(3)若体内的血药浓度不低于0.3毫克/升为药物有效时间,请你结合函数图象,直接指出该病人在注射后的药物有效时间为多少小时.
| t(小时) | 0 | 1 | 2 |
| y(毫克/升) | 0 | 0.14 | 0.24 |
(2)在注射后的第几小时,该病人体内的血药浓度达到最大?最大浓度是多少?
(3)若体内的血药浓度不低于0.3毫克/升为药物有效时间,请你结合函数图象,直接指出该病人在注射后的药物有效时间为多少小时.
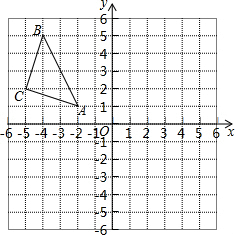 如图,△ABC在平面直角坐标系中,其中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).△ABC关于直线 l:x=-1对称的△A1B1C1,其中,点A、B、C的对应点分别为A1、B1、C1;
如图,△ABC在平面直角坐标系中,其中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).△ABC关于直线 l:x=-1对称的△A1B1C1,其中,点A、B、C的对应点分别为A1、B1、C1;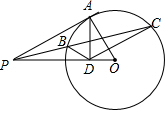 如图,PBC为⊙O的割线,AD⊥OP于点D,且∠APD=∠OAD
如图,PBC为⊙O的割线,AD⊥OP于点D,且∠APD=∠OAD